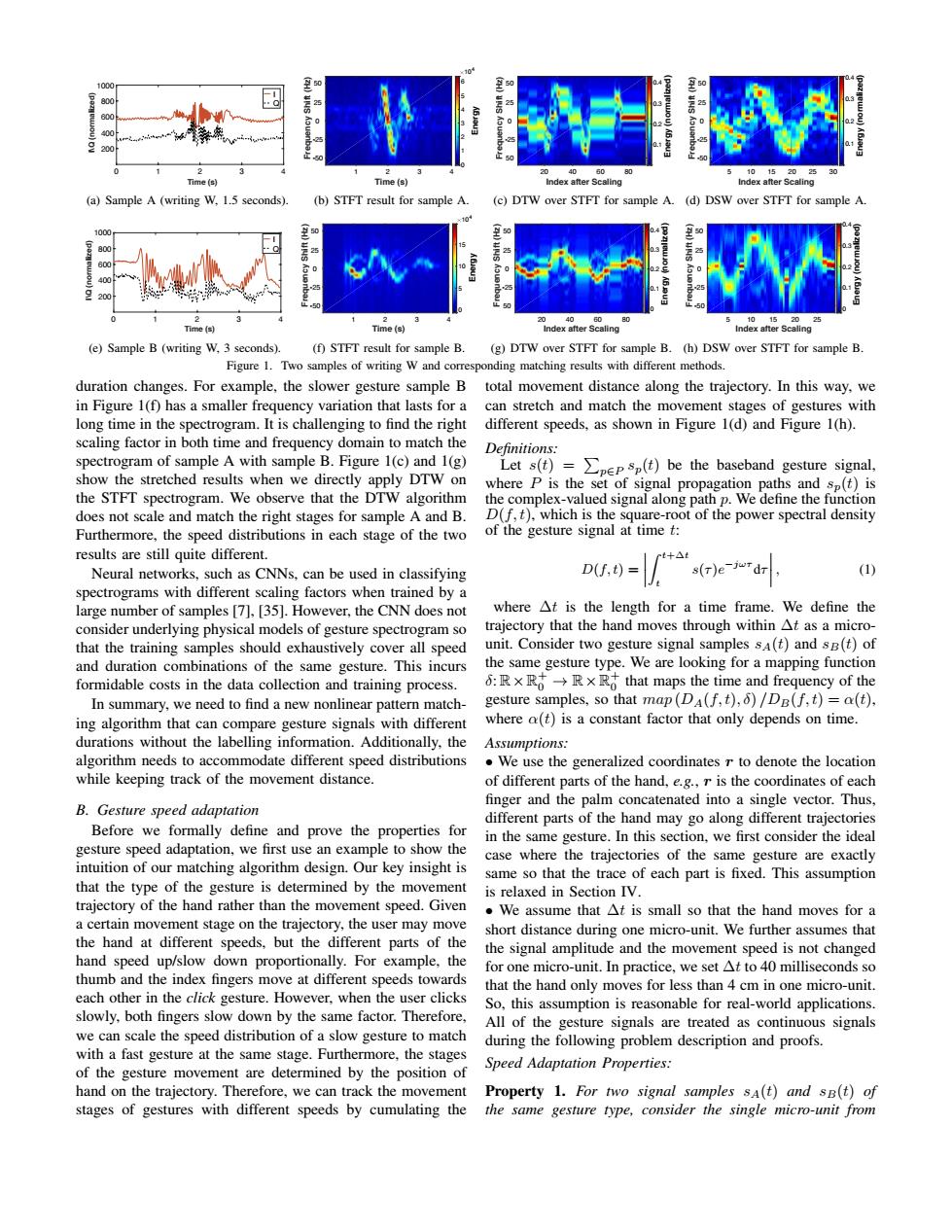
400 200 Time (s) Time(s) Index after Scaling (a)Sample A (writing W.1.5 seconds). (b)STFT result for sample A. (c)DTW over STFT for sample A. (d)DSW over STFT for sample A. 50 60 2 20 40 0 10 Time (s) Time(e倒 Index after Scaling Index after Scaling (e)Sample B(writing W,3 seconds). (f)STFT result for sample B. (g)DTW over STFT for sample B.(h)DSW over STFT for sample B. Figure 1.Two samples of writing W and corresponding matching results with different methods. duration changes.For example,the slower gesture sample B total movement distance along the trajectory.In this way,we in Figure 1(f)has a smaller frequency variation that lasts for a can stretch and match the movement stages of gestures with long time in the spectrogram.It is challenging to find the right different speeds,as shown in Figure 1(d)and Figure 1(h). scaling factor in both time and frequency domain to match the Definitions: spectrogram of sample A with sample B.Figure 1(c)and 1(g) Lets(t)= >pepsp(t)be the baseband gesture signal, show the stretched results when we directly apply DTW on where P is the set of signal propagation paths and sp(t)is the STFT spectrogram.We observe that the DTW algorithm the complex-valued signal along path p.We define the function does not scale and match the right stages for sample A and B. D(f,t),which is the square-root of the power spectral density Furthermore,the speed distributions in each stage of the two of the gesture signal at time t: results are still quite different. et+△t Neural networks,such as CNNs,can be used in classifying D(f,)= s(T)e-jwr (1) spectrograms with different scaling factors when trained by a large number of samples [7],[35].However,the CNN does not where At is the length for a time frame.We define the consider underlying physical models of gesture spectrogram so trajectory that the hand moves through within At as a micro- that the training samples should exhaustively cover all speed unit.Consider two gesture signal samples sA(t)and sB(t)of and duration combinations of the same gesture.This incurs the same gesture type.We are looking for a mapping function formidable costs in the data collection and training process. 6:R×Rt→R×R that maps the time and frequency of the In summary,we need to find a new nonlinear pattern match- gesture samples,so that map(DA(f,t),6)/DB(f,t)=a(t). ing algorithm that can compare gesture signals with different where a(t)is a constant factor that only depends on time. durations without the labelling information.Additionally,the Assumptions: algorithm needs to accommodate different speed distributions We use the generalized coordinates r to denote the location while keeping track of the movement distance. of different parts of the hand,e.g.,r is the coordinates of each finger and the palm concatenated into a single vector.Thus, B.Gesture speed adaptation different parts of the hand may go along different trajectories Before we formally define and prove the properties for in the same gesture.In this section,we first consider the ideal gesture speed adaptation,we first use an example to show the case where the trajectories of the same gesture are exactly intuition of our matching algorithm design.Our key insight is same so that the trace of each part is fixed.This assumption that the type of the gesture is determined by the movement is relaxed in Section IV. trajectory of the hand rather than the movement speed.Given We assume that At is small so that the hand moves for a a certain movement stage on the trajectory,the user may move short distance during one micro-unit.We further assumes that the hand at different speeds,but the different parts of the the signal amplitude and the movement speed is not changed hand speed up/slow down proportionally.For example,the for one micro-unit.In practice,we set At to 40 milliseconds so thumb and the index fingers move at different speeds towards that the hand only moves for less than 4 cm in one micro-unit. each other in the click gesture.However,when the user clicks So,this assumption is reasonable for real-world applications. slowly,both fingers slow down by the same factor.Therefore, All of the gesture signals are treated as continuous signals we can scale the speed distribution of a slow gesture to match during the following problem description and proofs. with a fast gesture at the same stage.Furthermore,the stages Speed Adaptation Properties: of the gesture movement are determined by the position of hand on the trajectory.Therefore,we can track the movement Property 1.For two signal samples sA(t)and sB(t)of stages of gestures with different speeds by cumulating the the same gesture type,consider the single micro-unit from01234 Time (s) 200 400 600 800 1000 I\Q (normalized) I Q (a) Sample A (writing W, 1.5 seconds). Energy 1234 Time (s) 50 25 0 -25 -50 Frequency Shift (Hz) 0 1 2 3 4 5 6 104 (b) STFT result for sample A. Energy (normalized) 20 40 60 80 Index after Scaling 50 25 0 -25 50 Frequency Shift (Hz) 0.1 0.2 0.3 0.4 (c) DTW over STFT for sample A. Energy (normalized) 5 10 15 20 25 30 Index after Scaling 50 25 0 -25 -50 Frequency Shift (Hz) 0.1 0.2 0.3 0.4 (d) DSW over STFT for sample A. 01234 Time (s) 200 400 600 800 1000 I\Q (normalized) I Q (e) Sample B (writing W, 3 seconds). Energy 1234 Time (s) 50 25 0 -25 -50 Frequency Shift (Hz) 0 5 10 15 104 (f) STFT result for sample B. Energy (normalized) 20 40 60 80 Index after Scaling 50 25 0 -25 50 Frequency Shift (Hz) 0 0.1 0.2 0.3 0.4 (g) DTW over STFT for sample B. Energy (normalized) 5 10 15 20 25 Index after Scaling 50 25 0 -25 -50 Frequency Shift (Hz) 0 0.1 0.2 0.3 0.4 (h) DSW over STFT for sample B. Figure 1. Two samples of writing W and corresponding matching results with different methods. duration changes. For example, the slower gesture sample B in Figure 1(f) has a smaller frequency variation that lasts for a long time in the spectrogram. It is challenging to find the right scaling factor in both time and frequency domain to match the spectrogram of sample A with sample B. Figure 1(c) and 1(g) show the stretched results when we directly apply DTW on the STFT spectrogram. We observe that the DTW algorithm does not scale and match the right stages for sample A and B. Furthermore, the speed distributions in each stage of the two results are still quite different. Neural networks, such as CNNs, can be used in classifying spectrograms with different scaling factors when trained by a large number of samples [7], [35]. However, the CNN does not consider underlying physical models of gesture spectrogram so that the training samples should exhaustively cover all speed and duration combinations of the same gesture. This incurs formidable costs in the data collection and training process. In summary, we need to find a new nonlinear pattern match￾ing algorithm that can compare gesture signals with different durations without the labelling information. Additionally, the algorithm needs to accommodate different speed distributions while keeping track of the movement distance. B. Gesture speed adaptation Before we formally define and prove the properties for gesture speed adaptation, we first use an example to show the intuition of our matching algorithm design. Our key insight is that the type of the gesture is determined by the movement trajectory of the hand rather than the movement speed. Given a certain movement stage on the trajectory, the user may move the hand at different speeds, but the different parts of the hand speed up/slow down proportionally. For example, the thumb and the index fingers move at different speeds towards each other in the click gesture. However, when the user clicks slowly, both fingers slow down by the same factor. Therefore, we can scale the speed distribution of a slow gesture to match with a fast gesture at the same stage. Furthermore, the stages of the gesture movement are determined by the position of hand on the trajectory. Therefore, we can track the movement stages of gestures with different speeds by cumulating the total movement distance along the trajectory. In this way, we can stretch and match the movement stages of gestures with different speeds, as shown in Figure 1(d) and Figure 1(h). Definitions: Let s(t) = P p2P sp(t) be the baseband gesture signal, where P is the set of signal propagation paths and sp(t) is the complex-valued signal along path p. We define the function D(f, t), which is the square-root of the power spectral density of the gesture signal at time t: D(f, t) = ￾ ￾ ￾ ￾ Z t+￾t t s(⌧ )e ￾j!⌧ d⌧ ￾ ￾ ￾ ￾ , (1) where ￾t is the length for a time frame. We define the trajectory that the hand moves through within ￾t as a micro￾unit. Consider two gesture signal samples sA(t) and sB(t) of the same gesture type. We are looking for a mapping function ￾: R⇥R+ 0 ! R⇥R+ 0 that maps the time and frequency of the gesture samples, so that map (DA(f, t), ￾) /DB(f, t) = ↵(t), where ↵(t) is a constant factor that only depends on time. Assumptions: • We use the generalized coordinates r to denote the location of different parts of the hand, e.g., r is the coordinates of each finger and the palm concatenated into a single vector. Thus, different parts of the hand may go along different trajectories in the same gesture. In this section, we first consider the ideal case where the trajectories of the same gesture are exactly same so that the trace of each part is fixed. This assumption is relaxed in Section IV. • We assume that ￾t is small so that the hand moves for a short distance during one micro-unit. We further assumes that the signal amplitude and the movement speed is not changed for one micro-unit. In practice, we set ￾t to 40 milliseconds so that the hand only moves for less than 4 cm in one micro-unit. So, this assumption is reasonable for real-world applications. All of the gesture signals are treated as continuous signals during the following problem description and proofs. Speed Adaptation Properties: Property 1. For two signal samples sA(t) and sB(t) of the same gesture type, consider the single micro-unit from