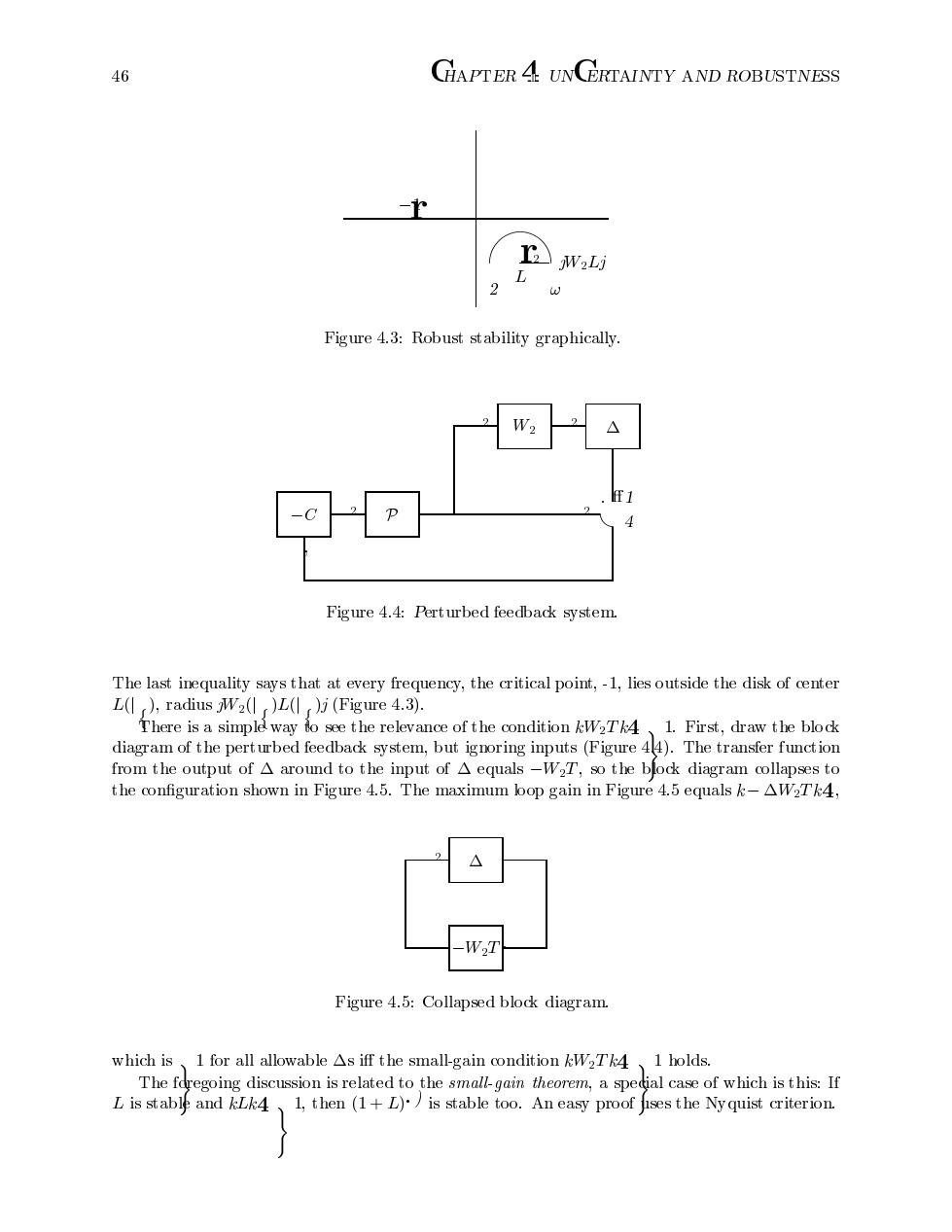
46 CHAPTER 4.UN ERTAINTY AND ROBUSTNESS r W2Lj 2 Figure 4.3:Robust stability graphically. W2 Figure 4.4:Perturbed feedback system The last inequality says that at every frequency,the critical point,-1,lies outside the disk of center L(),radius 2()L()j (Figure 4.3). There is a simple way io see the relevance of the condition kW2Tk4 1.First,draw the blodk diagram of the perturbed feedback system,but ignoring inputs(Figure 44).The transfer function from the output of A around to the input of A equals-W2T,so the block diagram collapses to the configuration shown in Figure 4.5.The maximum bop gain in Figure 4.5 equals k-AW2Tk4, W2T Figure 4.5:Collapsed block diagram. which is 1 for all allowable As iff the small-gain condition kW2Tk4 1 holds. The fdregoing discussion is related to the small-gain theorem,a special case of which is this:If L is stable and kLk4 1,then (1+L)/is stable too.An easy proof jises the Ny quist criterion. CHAPTER UNCERTAINTY AND ROBUSTNESS  r r ￾ jW￾Lj L  Figure  Robust stability graphically C P W￾  ￾ ￾ ￾ ￾ ￾  Figure  Perturbed feedback system The last inequality says that at every frequency the critical point  lies outside the disk of center Lj radius jW￾jLjj Figure  There is a simple way to see the relevance of the condition kW￾T k￾   First draw the block diagram of the perturbed feedback system but ignoring inputs Figure  The transfer function from the output of  around to the input of  equals W￾T  so the block diagram collapses to the conguration shown in Figure  The maximum loop gain in Figure  equals k W￾T k￾ W￾T ￾  Figure  Collapsed block diagram which is   for all allowable s i the smallgain condition kW￾T k￾   holds The foregoing discussion is related to the smal lgain theorem a special case of which is this If L is stable and kLk￾   then   L is stable too An easy proof uses the Nyquist criterion