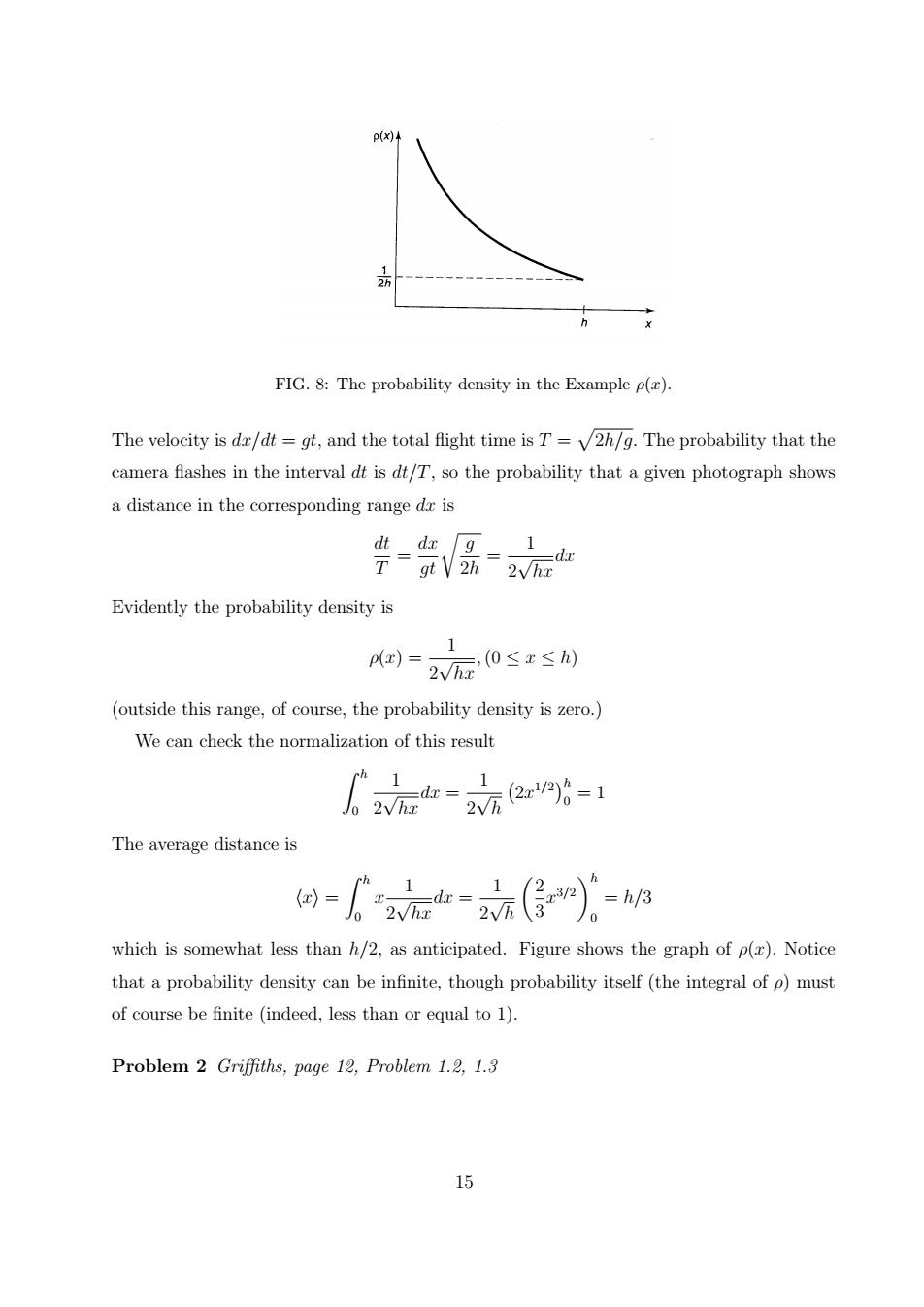
FIG.8:The probability density in the Example p(). The velocity is dr/dt=gt,and the total flight time is T=v2h/g.The probability that the camera flashes in the interval dt is dt/T,so the probability that a given photograph shows a distance in the corresponding range dr is dt dzg 1 T9元V2苏2VW Evidently the probability density is 1 回=2W后0≤r≤ (outside this range,of course,the probability density is zero.) We can check the normalization of this result Ch 1 1 人2wm=2w元2r6=1 The average distance is ==a(传心-咖 which is somewhat less than h/2,as anticipated.Figure shows the graph of p().Notice that a probability density can be infinite,though probability itself(the integral of p)must of course be finite (indeed,less than or equal to 1). Problem 2 Griffiths,page 12,Problem 1.2,1.3 15FIG. 8: The probability density in the Example ρ(x). The velocity is dx/dt = gt, and the total flight time is T = p 2h/g. The probability that the camera flashes in the interval dt is dt/T, so the probability that a given photograph shows a distance in the corresponding range dx is dt T = dx gt r g 2h = 1 2 √ hx dx Evidently the probability density is ρ(x) = 1 2 √ hx ,(0 ≤ x ≤ h) (outside this range, of course, the probability density is zero.) We can check the normalization of this result Z h 0 1 2 √ hx dx = 1 2 √ h ¡ 2x 1/2 ¢h 0 = 1 The average distance is hxi = Z h 0 x 1 2 √ hx dx = 1 2 √ h µ 2 3 x 3/2 ¶h 0 = h/3 which is somewhat less than h/2, as anticipated. Figure shows the graph of ρ(x). Notice that a probability density can be infinite, though probability itself (the integral of ρ) must of course be finite (indeed, less than or equal to 1). Problem 2 Griffiths, page 12, Problem 1.2, 1.3 15