正在加载图片...
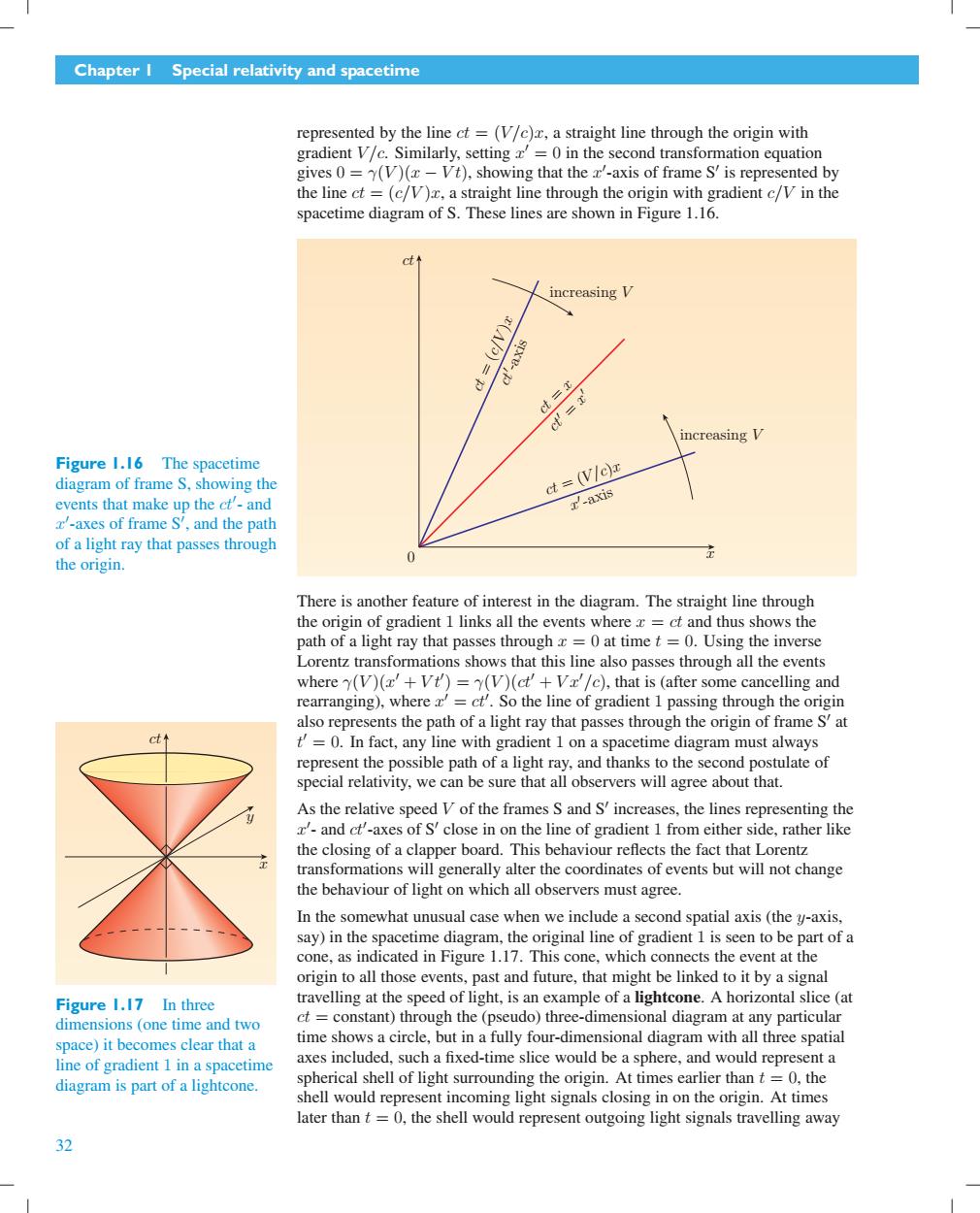
Chapter I Special relativity and spacetime represented by the line ct =(V/c),a straight line through the origin with gradient V/c.Similarly,setting '=0 in the second transformation equation gives 0=(V)(x-Vt),showing that the x'-axis of frame S'is represented by the line ct =(c/V),a straight line through the origin with gradient c/V in the spacetime diagram of S.These lines are shown in Figure 1.16. ct* 、increasing V (c/V)z ct'-axis ct =x ct'=x' increasing V Figure 1.16 The spacetime diagram of frame S,showing the ct =(V/c)z events that make up the ct'-and r'-axis z'-axes of frame S',and the path of a light ray that passes through the origin. 0 There is another feature of interest in the diagram.The straight line through the origin of gradient 1 links all the events where x=ct and thus shows the path of a light ray that passes through x=0 at time t=0.Using the inverse Lorentz transformations shows that this line also passes through all the events where (V)(x+Vt)=(V)(ct'+Vr'/c),that is (after some cancelling and rearranging),where c'=ct'.So the line of gradient 1 passing through the origin also represents the path of a light ray that passes through the origin of frame S'at ct t'=0.In fact,any line with gradient 1 on a spacetime diagram must always represent the possible path of a light ray,and thanks to the second postulate of special relativity,we can be sure that all observers will agree about that. As the relative speed V of the frames S and S'increases,the lines representing the '-and ct'-axes of S'close in on the line of gradient 1 from either side,rather like the closing of a clapper board.This behaviour reflects the fact that Lorentz transformations will generally alter the coordinates of events but will not change the behaviour of light on which all observers must agree. In the somewhat unusual case when we include a second spatial axis (the y-axis, say)in the spacetime diagram,the original line of gradient 1 is seen to be part of a cone,as indicated in Figure 1.17.This cone,which connects the event at the origin to all those events,past and future,that might be linked to it by a signal Figure 1.17 In three travelling at the speed of light,is an example of a lightcone.A horizontal slice (at dimensions (one time and two ct constant)through the(pseudo)three-dimensional diagram at any particular space)it becomes clear that a time shows a circle,but in a fully four-dimensional diagram with all three spatial line of gradient 1 in a spacetime axes included,such a fixed-time slice would be a sphere,and would represent a diagram is part of a lightcone. spherical shell of light surrounding the origin.At times earlier than t =0,the shell would represent incoming light signals closing in on the origin.At times later than t=0,the shell would represent outgoing light signals travelling away 32Chapter 1 Special relativity and spacetime represented by the line ct = (V /c)x, a straight line through the origin with gradient V /c. Similarly, setting x % = 0 in the second transformation equation gives 0 = γ(V )(x − V t), showing that the x % -axis of frame S % is represented by the line ct = (c/V )x, a straight line through the origin with gradient c/V in the spacetime diagram of S. These lines are shown in Figure 1.16. 0 x ct increasing V increasing V ct = (c/V )x ct = x ct " = x " ct = (V /c)x x " -axis ct " -axis Figure 1.16 The spacetime diagram of frame S, showing the events that make up the ct% - and x % -axes of frame S% , and the path of a light ray that passes through the origin. There is another feature of interest in the diagram. The straight line through the origin of gradient 1 links all the events where x = ct and thus shows the path of a light ray that passes through x = 0 at time t = 0. Using the inverse Lorentz transformations shows that this line also passes through all the events where γ(V )(x % + V t% ) = γ(V )(ct% + V x%/c), that is (after some cancelling and rearranging), where x % = ct% . So the line of gradient 1 passing through the origin also represents the path of a light ray that passes through the origin of frame S % at t % = 0. In fact, any line with gradient 1 on a spacetime diagram must always represent the possible path of a light ray, and thanks to the second postulate of special relativity, we can be sure that all observers will agree about that. As the relative speed V of the framesSand S % increases, the lines representing the x % - and ct% -axes of S % close in on the line of gradient 1 from either side, rather like the closing of a clapper board. This behaviour reflects the fact that Lorentz transformations will generally alter the coordinates of events but will not change the behaviour of light on which all observers must agree. In the somewhat unusual case when we include a second spatial axis (the y-axis, say) in the spacetime diagram, the original line of gradient 1 is seen to be part of a cone, as indicated in Figure 1.17. This cone, which connects the event at the origin to all those events, past and future, that might be linked to it by a signal travelling at the speed of light, is an example of a lightcone. A horizontal slice (at ct = constant) through the (pseudo) three-dimensional diagram at any particular time shows a circle, but in a fully four-dimensional diagram with all three spatial axes included, such a fixed-time slice would beasphere, and would represent a spherical shell of light surrounding the origin. At times earlier than t = 0, the shell would represent incoming light signals closing in on the origin. At times ct x y Figure 1.17 In three dimensions (one time and two space) it becomes clear that a line of gradient 1 in a spacetime diagram is part of a lightcone. later than t = 0, the shell would represent outgoing light signals travelling away 32