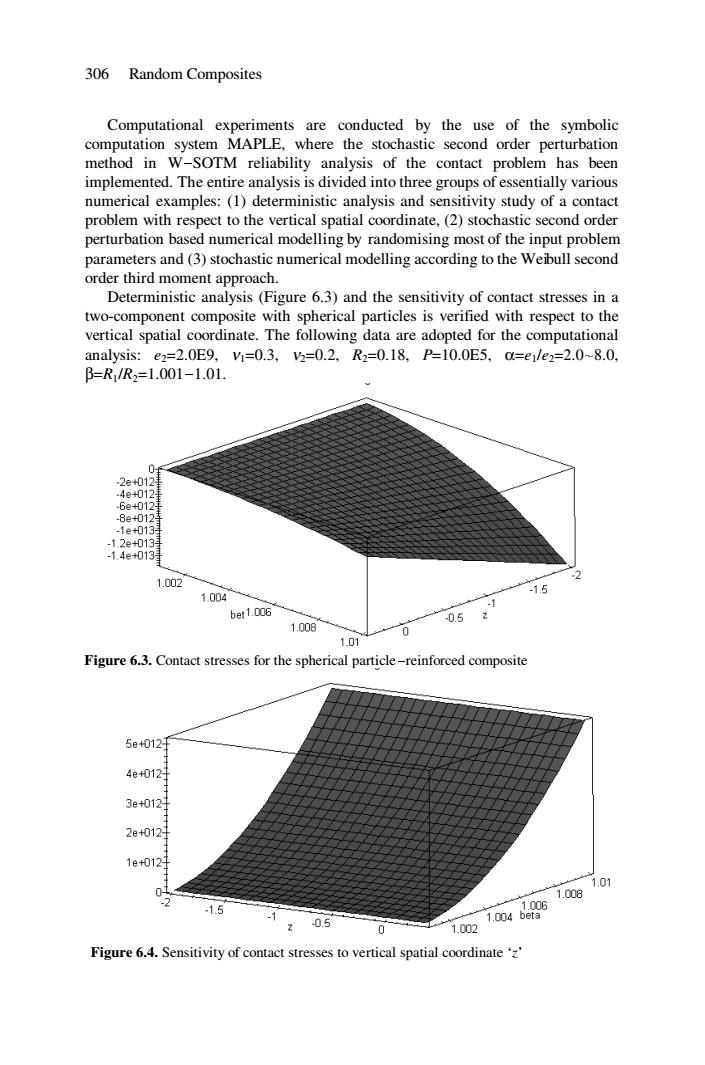
306 Random Composites Computational experiments are conducted by the use of the symbolic computation system MAPLE,where the stochastic second order perturbation method in W-SOTM reliability analysis of the contact problem has been implemented.The entire analysis is divided into three groups of essentially various numerical examples:(1)deterministic analysis and sensitivity study of a contact problem with respect to the vertical spatial coordinate,(2)stochastic second order perturbation based numerical modelling by randomising most of the input problem parameters and (3)stochastic numerical modelling according to the Weibull second order third moment approach. Deterministic analysis(Figure 6.3)and the sensitivity of contact stresses in a two-component composite with spherical particles is verified with respect to the vertical spatial coordinate.The following data are adopted for the computational analysis:.e2=2.0E9,1=0.3,2=0.2,R2=0.18,P=10.0E5,0=e1/e2=2.0~8.0, B=R/R2=1.001-1.01. 0 -2e012 .4e+0121 -6e+012 -8e+012 -1e013月 -1.2e013 -1.4e013 2 1.002 -1.5 1.004 bet1.006 -0.52 1.008 0 1.01 Figure 6.3.Contact stresses for the spherical particle-reinforced composite 5e0121 4e+012 3e+012 2e+0121 1e+012 0 1.008 1.01 2 -1.5 1.006 -1 z0.5 1.004 beta 0 1.002 Figure 6.4.Sensitivity of contact stresses to vertical spatial coordinate''306 Random Composites Computational experiments are conducted by the use of the symbolic computation system MAPLE, where the stochastic second order perturbation method in W-SOTM reliability analysis of the contact problem has been implemented. The entire analysis is divided into three groups of essentially various numerical examples: (1) deterministic analysis and sensitivity study of a contact problem with respect to the vertical spatial coordinate, (2) stochastic second order perturbation based numerical modelling by randomising most of the input problem parameters and (3) stochastic numerical modelling according to the Weibull second order third moment approach. Deterministic analysis (Figure 6.3) and the sensitivity of contact stresses in a two-component composite with spherical particles is verified with respect to the vertical spatial coordinate. The following data are adopted for the computational analysis: e2=2.0E9, ν1=0.3, ν2=0.2, R2=0.18, P=10.0E5, α=e1/e2=2.0~8.0, β=R1/R2=1.001-1.01. Figure 6.3. Contact stresses for the spherical particle-reinforced composite Figure 6.4. Sensitivity of contact stresses to vertical spatial coordinate ‘z’