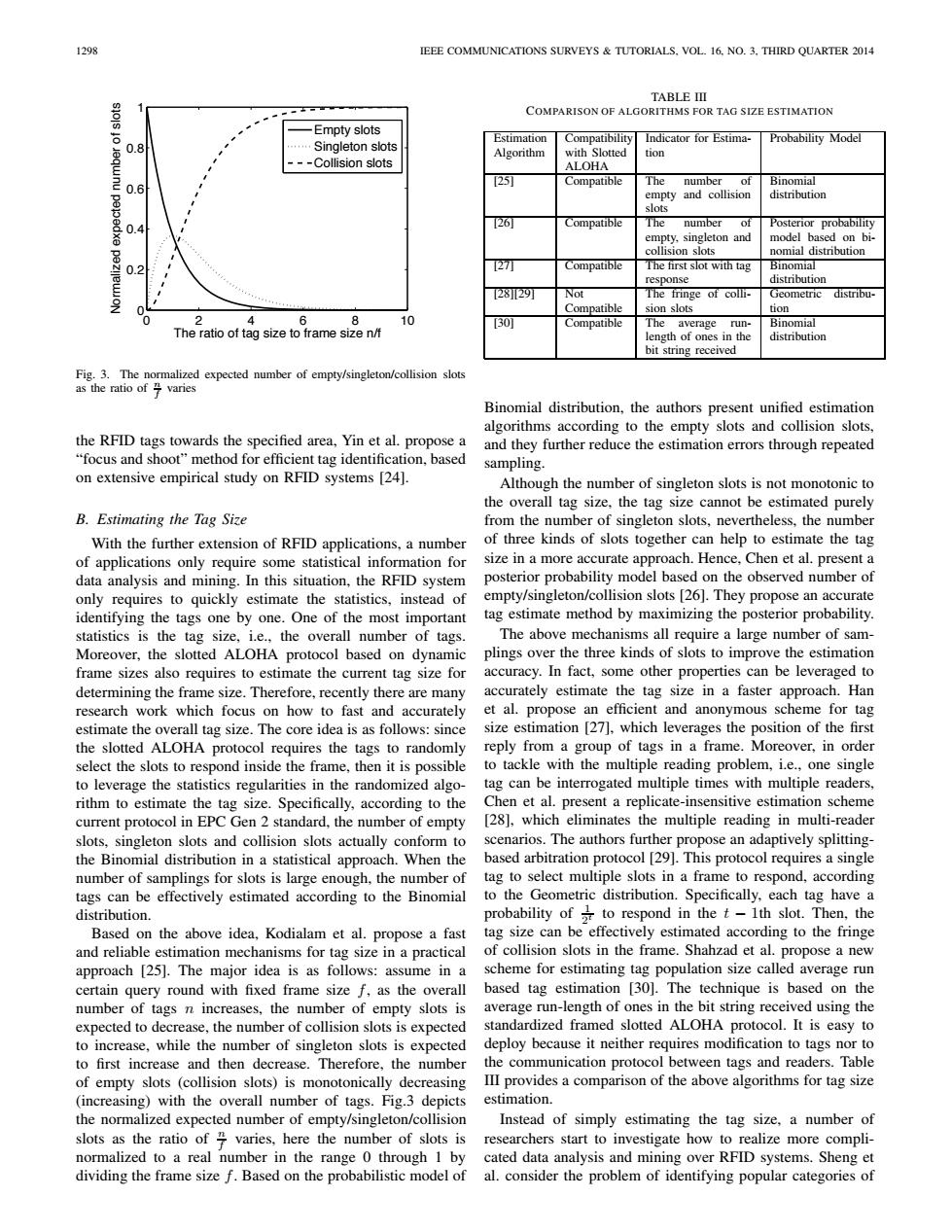
1298 IEEE COMMUNICATIONS SURVEYS TUTORIALS.VOL.16.NO.3.THIRD QUARTER 2014 TABLE III COMPARISON OF ALGORITHMS FOR TAG SIZE ESTIMATION Empty slots Estimation Compatibility Indicator for Estima- Probability Model 0.8 Singleton slots Algorithm with Slotted tion -Collision slots ALOHA 25 Compatible The number of Binomial 0.6 empty and collision distribution slots 0.4 26 Compatible The number of Posterior probability empty,singleton and model based on bi- collision slots nomial distribution 0.2 127 Compatible The first slot with tag Binomial response distribution T2829 Not The fringe of colli- Geometric distribu- 0 Compatible sion slots tion 2 6 8 10 [30 Compatible The average run- Binomial The ratio of tag size to frame size n/f length of ones in the distribution bit string received Fig.3.The normalized expected number of empty/singleton/collision slots as the ratio of子varies Binomial distribution,the authors present unified estimation algorithms according to the empty slots and collision slots, the RFID tags towards the specified area,Yin et al.propose a and they further reduce the estimation errors through repeated "focus and shoot"method for efficient tag identification,based sampling on extensive empirical study on RFID systems [24]. Although the number of singleton slots is not monotonic to the overall tag size,the tag size cannot be estimated purely B.Estimating the Tag Size from the number of singleton slots,nevertheless,the number With the further extension of RFID applications,a number of three kinds of slots together can help to estimate the tag of applications only require some statistical information for size in a more accurate approach.Hence,Chen et al.present a data analysis and mining.In this situation,the RFID system posterior probability model based on the observed number of only requires to quickly estimate the statistics,instead of empty/singleton/collision slots [26].They propose an accurate identifying the tags one by one.One of the most important tag estimate method by maximizing the posterior probability. statistics is the tag size,i.e.,the overall number of tags. The above mechanisms all require a large number of sam- Moreover,the slotted ALOHA protocol based on dynamic plings over the three kinds of slots to improve the estimation frame sizes also requires to estimate the current tag size for accuracy.In fact,some other properties can be leveraged to determining the frame size.Therefore,recently there are many accurately estimate the tag size in a faster approach.Han research work which focus on how to fast and accurately et al.propose an efficient and anonymous scheme for tag estimate the overall tag size.The core idea is as follows:since size estimation [27],which leverages the position of the first the slotted ALOHA protocol requires the tags to randomly reply from a group of tags in a frame.Moreover,in order select the slots to respond inside the frame,then it is possible to tackle with the multiple reading problem,i.e.,one single to leverage the statistics regularities in the randomized algo- tag can be interrogated multiple times with multiple readers, rithm to estimate the tag size.Specifically,according to the Chen et al.present a replicate-insensitive estimation scheme current protocol in EPC Gen 2 standard,the number of empty [28],which eliminates the multiple reading in multi-reader slots,singleton slots and collision slots actually conform to scenarios.The authors further propose an adaptively splitting- the Binomial distribution in a statistical approach.When the based arbitration protocol [29].This protocol requires a single number of samplings for slots is large enough,the number of tag to select multiple slots in a frame to respond,according tags can be effectively estimated according to the Binomial to the Geometric distribution.Specifically,each tag have a distribution. probability of to respond in the t-1th slot.Then,the Based on the above idea,Kodialam et al.propose a fast tag size can be effectively estimated according to the fringe and reliable estimation mechanisms for tag size in a practical of collision slots in the frame.Shahzad et al.propose a new approach [25].The major idea is as follows:assume in a scheme for estimating tag population size called average run certain query round with fixed frame size f,as the overall based tag estimation [30].The technique is based on the number of tags n increases,the number of empty slots is average run-length of ones in the bit string received using the expected to decrease,the number of collision slots is expected standardized framed slotted ALOHA protocol.It is easy to to increase,while the number of singleton slots is expected deploy because it neither requires modification to tags nor to to first increase and then decrease.Therefore,the number the communication protocol between tags and readers.Table of empty slots (collision slots)is monotonically decreasing III provides a comparison of the above algorithms for tag size (increasing)with the overall number of tags.Fig.3 depicts estimation. the normalized expected number of empty/singleton/collision Instead of simply estimating the tag size,a number of slots as the ratio of4 varies,here the number of slots is researchers start to investigate how to realize more compli- normalized to a real number in the range 0 through I by cated data analysis and mining over RFID systems.Sheng et dividing the frame size f.Based on the probabilistic model of al.consider the problem of identifying popular categories of1298 IEEE COMMUNICATIONS SURVEYS & TUTORIALS, VOL. 16, NO. 3, THIRD QUARTER 2014 0 2 4 6 8 10 0 0.2 0.4 0.6 0.8 1 The ratio of tag size to frame size n/f Normalized expected number of slots Empty slots Singleton slots Collision slots Fig. 3. The normalized expected number of empty/singleton/collision slots as the ratio of n f varies the RFID tags towards the specified area, Yin et al. propose a “focus and shoot” method for efficient tag identification, based on extensive empirical study on RFID systems [24]. B. Estimating the Tag Size With the further extension of RFID applications, a number of applications only require some statistical information for data analysis and mining. In this situation, the RFID system only requires to quickly estimate the statistics, instead of identifying the tags one by one. One of the most important statistics is the tag size, i.e., the overall number of tags. Moreover, the slotted ALOHA protocol based on dynamic frame sizes also requires to estimate the current tag size for determining the frame size. Therefore, recently there are many research work which focus on how to fast and accurately estimate the overall tag size. The core idea is as follows: since the slotted ALOHA protocol requires the tags to randomly select the slots to respond inside the frame, then it is possible to leverage the statistics regularities in the randomized algo￾rithm to estimate the tag size. Specifically, according to the current protocol in EPC Gen 2 standard, the number of empty slots, singleton slots and collision slots actually conform to the Binomial distribution in a statistical approach. When the number of samplings for slots is large enough, the number of tags can be effectively estimated according to the Binomial distribution. Based on the above idea, Kodialam et al. propose a fast and reliable estimation mechanisms for tag size in a practical approach [25]. The major idea is as follows: assume in a certain query round with fixed frame size f, as the overall number of tags n increases, the number of empty slots is expected to decrease, the number of collision slots is expected to increase, while the number of singleton slots is expected to first increase and then decrease. Therefore, the number of empty slots (collision slots) is monotonically decreasing (increasing) with the overall number of tags. Fig.3 depicts the normalized expected number of empty/singleton/collision slots as the ratio of n f varies, here the number of slots is normalized to a real number in the range 0 through 1 by dividing the frame size f. Based on the probabilistic model of TABLE III COMPARISON OF ALGORITHMS FOR TAG S IZE ESTIMATION Estimation Algorithm Compatibility with Slotted ALOHA Indicator for Estima￾tion Probability Model [25] Compatible The number of empty and collision slots Binomial distribution [26] Compatible The number of empty, singleton and collision slots Posterior probability model based on bi￾nomial distribution [27] Compatible The first slot with tag response Binomial distribution [28][29] Not Compatible The fringe of colli￾sion slots Geometric distribu￾tion [30] Compatible The average run￾length of ones in the bit string received Binomial distribution Binomial distribution, the authors present unified estimation algorithms according to the empty slots and collision slots, and they further reduce the estimation errors through repeated sampling. Although the number of singleton slots is not monotonic to the overall tag size, the tag size cannot be estimated purely from the number of singleton slots, nevertheless, the number of three kinds of slots together can help to estimate the tag size in a more accurate approach. Hence, Chen et al. present a posterior probability model based on the observed number of empty/singleton/collision slots [26]. They propose an accurate tag estimate method by maximizing the posterior probability. The above mechanisms all require a large number of sam￾plings over the three kinds of slots to improve the estimation accuracy. In fact, some other properties can be leveraged to accurately estimate the tag size in a faster approach. Han et al. propose an efficient and anonymous scheme for tag size estimation [27], which leverages the position of the first reply from a group of tags in a frame. Moreover, in order to tackle with the multiple reading problem, i.e., one single tag can be interrogated multiple times with multiple readers, Chen et al. present a replicate-insensitive estimation scheme [28], which eliminates the multiple reading in multi-reader scenarios. The authors further propose an adaptively splitting￾based arbitration protocol [29]. This protocol requires a single tag to select multiple slots in a frame to respond, according to the Geometric distribution. Specifically, each tag have a probability of 1 2t to respond in the t − 1th slot. Then, the tag size can be effectively estimated according to the fringe of collision slots in the frame. Shahzad et al. propose a new scheme for estimating tag population size called average run based tag estimation [30]. The technique is based on the average run-length of ones in the bit string received using the standardized framed slotted ALOHA protocol. It is easy to deploy because it neither requires modification to tags nor to the communication protocol between tags and readers. Table III provides a comparison of the above algorithms for tag size estimation. Instead of simply estimating the tag size, a number of researchers start to investigate how to realize more compli￾cated data analysis and mining over RFID systems. Sheng et al. consider the problem of identifying popular categories of