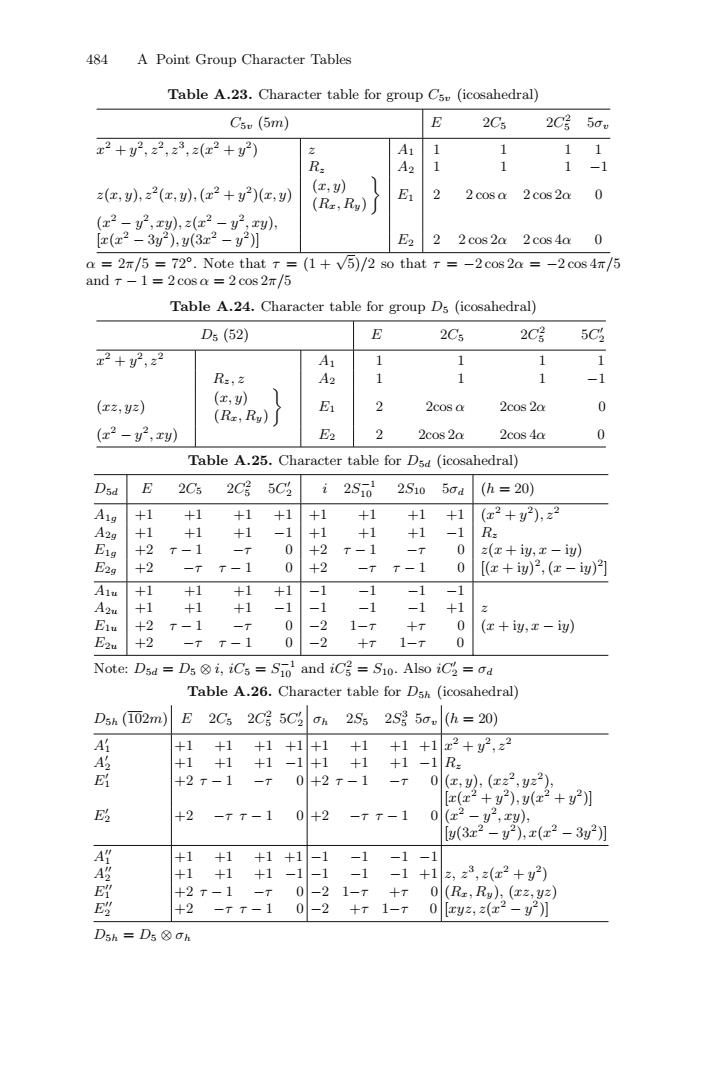
484 A Point Group Character Tables Table A.23.Character table for group Cse (icosahedral) Csu(5m) E 2Cs 2C号5am x2+y2,22,z3,z(2+） A 1 1 1 1 R: A2 1 1 1 -1 z(x,),2(x,,(x2+y2)(x,) (x,) E 2 2 cosa 2cos 2a (Rz,Ry) 0 (x2-y2,xy),z2(x2-y2,xy) [z(x2-3y2),y(3z2-y2】 E2 2 2 cos 2a 2cos4a 0 a =2/5 =72.Note that T =(1+v5)/2 so that T =-2cos 2a =-2 cos 4/5 and T-1 2 cosa 2 cos 2/5 Table A.24.Character table for group Ds (icosahedral) D5(52) E 2C5 2C号 5C x2+y,22 1 义 1 1 R=,z A2 1 2 1 -1 (x,y） (xz,yz) E 2 2cos a 2cos 20 0 (Rx,Ry） (x2-2,x) E2 2 2cos 2a 2cos 4a 0 Table A.25. Character table for Dsd (icosahedral) Dsd E 2C5 2C号 5C2 2S10 2S10 50d (h=20) A1g +1 +1 +1 +1 +1 +1 +1 +1 (x2+y),z2 A2g +1 +1 +1 -1 +1 +1 +1 -1 Ra E1s +2 T-1 -T 0 +2 r-1 -T 0 z(x+iy,x-iy) E2g +2 一T T-1 0 +2 -T T-1 0 [(x+ig)2,(x-iy)] Alu +1 +1 +1 +1 -1 -1 -1 -1 A2u +1 +1 +1 -1 -1 -1 -1 +1 E +2 T-1 一T 0 -2 1-T +T 0 (x+iy,x-iy） E2u +2 一T T-1 0 -2 +T 1-T 0 Note:Dsd Ds i,ics Sio and ic=S10.Also iC=d Table A.26.Character table for Dsh (icosahedral) Dsh (102m) E 2C5 2C号5C2 Oh 2S5 2S%5a.(h=20) A +1 +1 +1+1+1 +1 +1+1x2+y2,22 A +1 +1 +1-1+1 +1 +1-1 R: E +2T-1 一T 0+2T-1 -T0(x,,(x22,y22, z(2+y2),(x2+2】 的 +2 -TT-1 0+2 -rT-1 0(x2-y,xy, y(3x2-y2),x(x2-3y2】 +1 +1 +1+1 -1 -1 -1-1 A码 +1 +1 +1-1-1-1 -1+1 2,23,z(x2+2) +2T-1 一T 0-2 1-T +7 0(Rz;Ry),(xz,yz) +2 -TT-1 0 -2 十T 1-r [xy2,2(x2-y] D5h=D5⑧h484 A Point Group Character Tables Table A.23. Character table for group C5v (icosahedral) C5v (5m) E 2C5 2C2 5 5σv x2 + y2, z2, z3, z(x2 + y2) z A1 1 1 11 Rz A2 1 11 −1 z(x, y), z2(x, y),(x2 + y2)(x, y) (x, y) (Rx, Ry) " E1 2 2 cos α 2 cos 2α 0 (x2 − y2, xy), z(x2 − y2, xy), [x(x2 − 3y2), y(3x2 − y2)] E2 2 2 cos 2α 2 cos 4α 0 α = 2π/5 = 72◦. Note that τ = (1 + √5)/2 so that τ = −2 cos 2α = −2 cos 4π/5 and τ − 1 = 2 cos α = 2 cos 2π/5 Table A.24. Character table for group D5 (icosahedral) D5 (52) E 2C5 2C2 5 5C 2 x2 + y2, z2 A1 1 1 11 Rz, z A2 111 −1 (xz, yz) (x, y) (Rx, Ry) " E1 2 2cos α 2cos 2α 0 (x2 − y2, xy) E2 2 2cos 2α 2cos 4α 0 Table A.25. Character table for D5d (icosahedral) D5d E 2C5 2C2 5 5C 2 i 2S−1 10 2S10 5σd (h = 20) A1g +1 +1 +1 +1 +1 +1 +1 +1 (x2 + y2), z2 A2g +1 +1 +1 −1 +1 +1 +1 −1 Rz E1g +2 τ − 1 −τ 0 +2 τ − 1 −τ 0 z(x + iy, x − iy) E2g +2 −τ τ − 1 0 +2 −τ τ − 1 0 [(x + iy) 2,(x − iy) 2] A1u +1 +1 +1 +1 −1 −1 −1 −1 A2u +1 +1 +1 −1 −1 −1 −1 +1 z E1u +2 τ − 1 −τ 0 −2 1−τ +τ 0 (x + iy, x − iy) E2u +2 −τ τ − 1 0 −2 +τ 1−τ 0 Note: D5d = D5 ⊗ i, iC5 = S−1 10 and iC2 5 = S10. Also iC 2 = σd Table A.26. Character table for D5h (icosahedral) D5h (102m) E 2C5 2C2 5 5C 2 σh 2S5 2S3 5 5σv (h = 20) A 1 +1 +1 +1 +1 +1 +1 +1 +1 x2 + y2, z2 A 2 +1 +1 +1 −1 +1 +1 +1 −1 Rz E 1 +2 τ − 1 −τ 0 +2 τ − 1 −τ 0 (x, y), (xz2, yz2), [x(x2 + y2), y(x2 + y2)] E 2 +2 −τ τ − 1 0 +2 −τ τ − 1 0 (x2 − y2, xy), [y(3x2 − y2), x(x2 − 3y2)] A 1 +1 +1 +1 +1 −1 −1 −1 −1 A 2 +1 +1 +1 −1 −1 −1 −1 +1 z, z3, z(x2 + y2) E 1 +2 τ − 1 −τ 0 −2 1−τ +τ 0 (Rx, Ry), (xz, yz) E 2 +2 −τ τ − 1 0 −2 +τ 1−τ 0 [xyz, z(x2 − y2)] D5h = D5 ⊗ σh