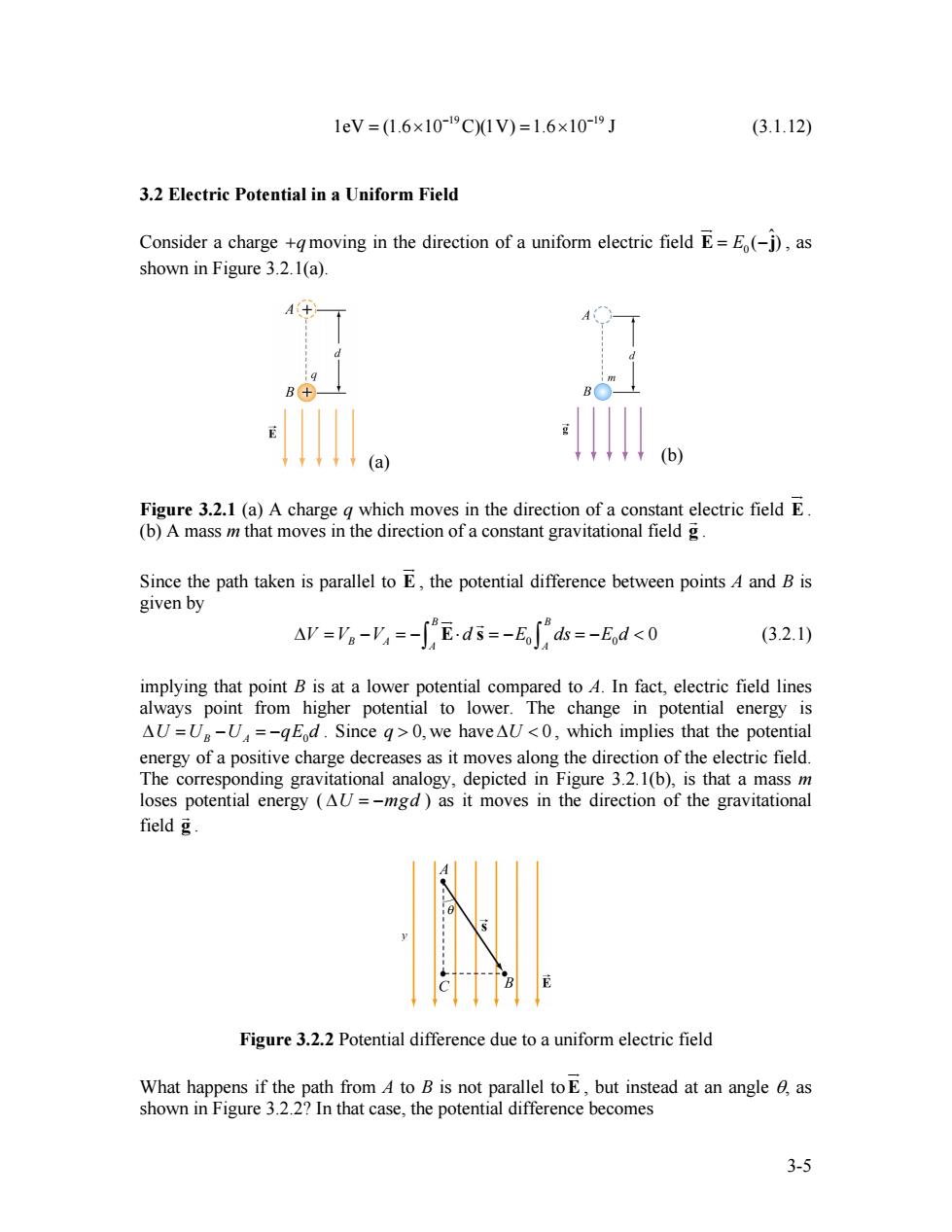
1eV=(1.6×10-19C)1V)=1.6×10-19J (3.1.12) 3.2 Electric Potential in a Uniform Field Consider a charge +gmoving in the direction of a uniform electric field E=E(-j),as shown in Figure 3.2.1(a). A B (a) (b) Figure 3.2.1(a)A charge g which moves in the direction of a constant electric field E. (b)A mass m that moves in the direction of a constant gravitational field g. Since the path taken is parallel to E,the potential difference between points A and B is given by AV=。-y,=-∫Eds=-Es=-Ed<0 (3.2.1) implying that point B is at a lower potential compared to 4.In fact,electric field lines always point from higher potential to lower.The change in potential energy is AU=U-U=-gEd.Since g>0,we haveAU<0,which implies that the potential energy of a positive charge decreases as it moves along the direction of the electric field. The corresponding gravitational analogy,depicted in Figure 3.2.1(b),is that a mass m loses potential energy (AU =-mgd )as it moves in the direction of the gravitational field g. Figure 3.2.2 Potential difference due to a uniform electric field What happens if the path from 4 to B is not parallel toE,but instead at an angle e,as shown in Figure 3.2.2?In that case,the potential difference becomes 3-5(3.1.12) 19 19 1eV (1.6 10 C)(1V) 1.6 10 J − = × = × − 3.2 Electric Potential in a Uniform Field Consider a charge +q moving in the direction of a uniform electric field 0 ˆ E = E (−j) JG , as shown in Figure 3.2.1(a). (a) (b) Figure 3.2.1 (a) A charge q which moves in the direction of a constant electric field E JG . (b) A mass m that moves in the direction of a constant gravitational field g G . Since the path taken is parallel to E JG , the potential difference between points A and B is given by 0 0 0 B B B A A A ∆V V= −V = − ⋅ d = −E ds = −E d < ∫ ∫ E s JG G (3.2.1) implying that point B is at a lower potential compared to A. In fact, electric field lines always point from higher potential to lower. The change in potential energy is . Since we have U UB A U 0 ∆ =−= −qE d q > 0, ∆U < 0 , which implies that the potential energy of a positive charge decreases as it moves along the direction of the electric field. The corresponding gravitational analogy, depicted in Figure 3.2.1(b), is that a mass m loses potential energy ( ) as it moves in the direction of the gravitational field ∆ = U −mgd g G . Figure 3.2.2 Potential difference due to a uniform electric field What happens if the path from A to B is not parallel toE JG , but instead at an angle θ, as shown in Figure 3.2.2? In that case, the potential difference becomes 3-5