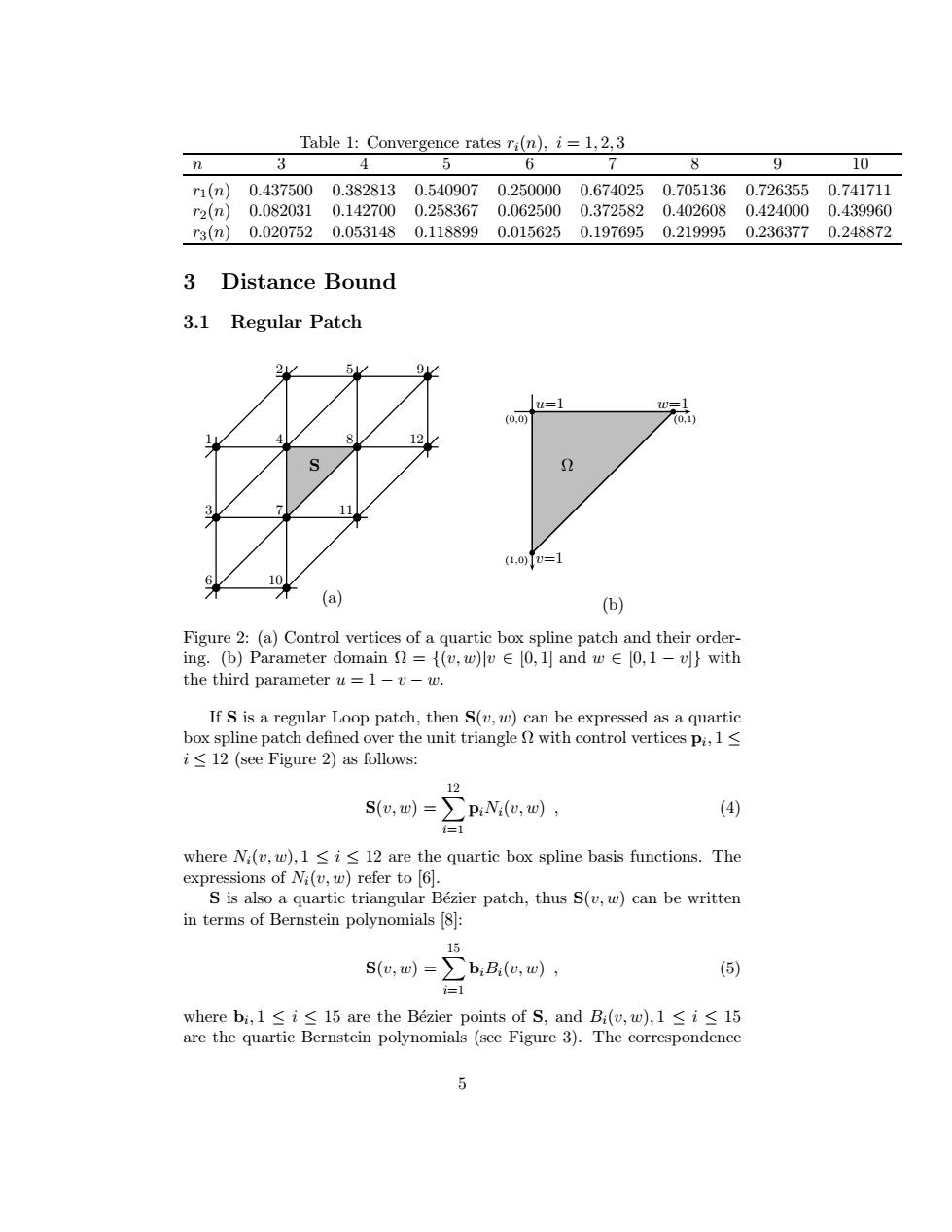
Table 1:Comvergeace rates r)12.3 8 0 3 Distance Bound 3.1 Regular Patch (a} b e quartic box spline basis functions.The 5,-∑h,m (5Table 1: Convergence rates ri(n), i = 1, 2, 3 n 3 4 5 6 7 8 9 10 r1(n) 0.437500 0.382813 0.540907 0.250000 0.674025 0.705136 0.726355 0.741711 r2(n) 0.082031 0.142700 0.258367 0.062500 0.372582 0.402608 0.424000 0.439960 r3(n) 0.020752 0.053148 0.118899 0.015625 0.197695 0.219995 0.236377 0.248872 3 Distance Bound 3.1 Regular Patch b b b b b b b b b 2 5 9 b b b 1 4 8 12 3 7 11 6 10 S (a) b b b Ω (0,0) u=1 (0,1) (1,0) w=1 v=1 (b) Figure 2: (a) Control vertices of a quartic box spline patch and their order￾ing. (b) Parameter domain Ω = {(v, w)|v ∈ [0, 1] and w ∈ [0, 1 − v]} with the third parameter u = 1 − v − w. If S is a regular Loop patch, then S(v, w) can be expressed as a quartic box spline patch defined over the unit triangle Ω with control vertices pi , 1 ≤ i ≤ 12 (see Figure 2) as follows: S(v, w) = X 12 i=1 piNi(v, w) , (4) where Ni(v, w), 1 ≤ i ≤ 12 are the quartic box spline basis functions. The expressions of Ni(v, w) refer to [6]. S is also a quartic triangular B´ezier patch, thus S(v, w) can be written in terms of Bernstein polynomials [8]: S(v, w) = X 15 i=1 biBi(v, w) , (5) where bi , 1 ≤ i ≤ 15 are the B´ezier points of S, and Bi(v, w), 1 ≤ i ≤ 15 are the quartic Bernstein polynomials (see Figure 3). The correspondence 5