正在加载图片...
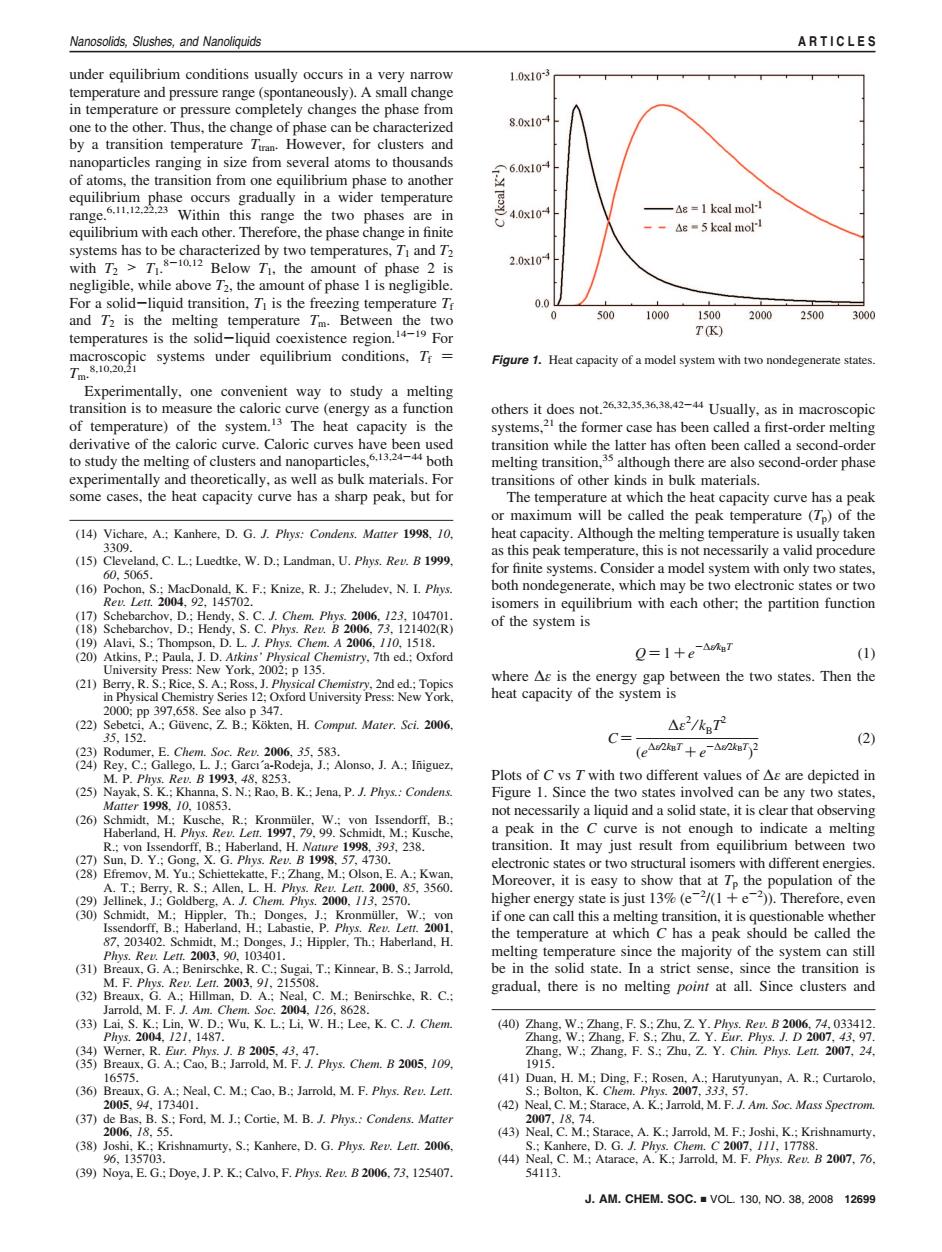
Nanosolids,Slushes,and Nanoliquids ARTICLES under equilibrium conditions usually occurs in a very narrow 1.0x10 temperature and pressure range (spontaneously).A small change in temperature or pressure completely changes the phase from one to the other.Thus,the change of phase can be characterized 8.0x10A by a transition temperature Tiran.However,for clusters and nanoparticles ranging in size from several atoms to thousands 今6.0x10 of atoms,the transition from one equilibrium phase to another equilibrium phase occurs gradually in a wider temperature range.11.122 Within this range the two phases are in 4.0x10 —A8=1 keal moll equilibrium with each other.Therefore,the phase change in finite --△s=5 keal moll systems has to be characterized by two temperatures,T1 and T2 with T2>T1.8-10.12 Below T1.the amount of phase 2 is 2.0x10 negligible,while above 72,the amount of phase I is negligible. For a solid-liquid transition.T is the freezing temperature Tr 0.0 and T2 is the melting temperature Tm.Between the two 0 500 1000 1500 2000 2500 3000 temperatures is the solid-liquid coexistence region.419 For TK) macroscopic systems under equilibrium conditions,Tr= Figure 1.Heat capacity of a model system with two nondegenerate states. Tm.8.10,20.2 Experimentally,one convenient way to study a melting transition is to measure the caloric curve (energy as a function others it does not.26.32.35.36.38.2-44 Usually,as in macroscopic of temperature)of the system.13 The heat capacity is the systems,21 the former case has been called a first-order melting derivative of the caloric curve.Caloric curves have been used transition while the latter has often been called a second-order to study the melting of clusters and nanoparticles,.3.24-4 both melting transition,35 although there are also second-order phase experimentally and theoretically,as well as bulk materials.For transitions of other kinds in bulk materials. some cases,the heat capacity curve has a sharp peak,but for The temperature at which the heat capacity curve has a peak or maximum will be called the peak temperature (T)of the (14)Vichare,A.:Kanhere,D.G.J.Plys:Condens.Matter 1998,10, heat capacity.Although the melting temperature is usually taken 3309. as this peak temperature,this is not necessarily a valid procedure (15)Cleveland.C.L.:Luedtke.W.D.:Landman,U.Phys.Rev.B 1999. 60.5065. for finite systems.Consider a model system with only two states. (16)Pochon,S.:MacDonald,K.F.:Knize,R.J.:Zheludev,N.I.Plrys. both nondegenerate,which may be two electronic states or two Reu.Let.2004,92.145702. isomers in equilibrium with each other:the partition function (17)Schebarchov.D.:Hendy.S.C.J.Chem.Phrys.2006.123.104701. (18)Schebarchov,D.:Hendy,S.C.Plrys.Rev.B 2006,73,121402(R) of the system is (19)Alavi,S.:Thompson.D.L.J.Phrys.Chem.A 2006.110,1518. (20)Atkins,P.:Paula,J.D.Atkins'Phrysical Chemistry,7th ed.;Oxford Q=1+e-a7 (1) University Press:New York,2002;p 135. (21)Berry.R.S.:Rice.S.A.:Ross.J.Physical Chemistry.2nd ed.:Topics where As is the energy gap between the two states.Then the in Physical Chemistry Series 12:Oxford University Press:New York. heat capacity of the system is 2000,Pp397,658.See also p347. (22)Sebetci,A.:Guvenc,Z.B.:Kokten.H.Comput.Mater.Sci.2006. △e2/kTr2 35,152. C= (2) (23)Rodumer.E.Chem.Soc.Rev.2006.35.583. (eAukaT+e-AukBT2 (24)Rey,C.:Gallego,L.J.:Garci'a-Rodeja,J.;Alonso.J.A.:Iniguez, M.P.Pys.Reu.B1993.48.8253. Plots of C vs T with two different values of As are depicted in (25)Nayak.S.K.;Khanna,S.N.;Rao.B.K.:Jena,P.J.Phys.:Condens. Figure 1.Since the two states involved can be any two states. Matter1998.10,10853. (26)Schmidt.M.:Kusche.R.:Kronmuiler.W.:von Issendorff.B.: not necessarily a liquid and a solid state,it is clear that observing Haberland,H.Phys.Rev.Lett.1997,79.99.Schmidt,M.;Kusche, a peak in the C curve is not enough to indicate a melting R.:von Issendorff,B.:Haberland,H.Nature 1998.393.238. transition.It may just result from equilibrium between two (27)Sun,D.Y.:Gong,X.G.Phys.Rev.B 1998,57,4730. electronic states or two structural isomers with different energies. (28)Efremov,M.Yu.:Schiettekatte,F.;Zhang,M.;Olson,E.A.:Kwan, A.T.;Berry,R.S.:Allen,L.H.Phys.Rev.Lett.2000,85,3560. Moreover,it is easy to show that at To the population of the (29)Jellinek,J.:Goldberg.A.J.Chem.Phys.2000.113.2570. higher energy state is just 13%(e2/(1+e)).Therefore,even (30)Schmidt,M.:Hippler,Th.:Donges,J.;Kronmuller,W.;von if one can call this a melting transition,it is questionable whether Issendorff,B.:Haberland,H.:Labastie,P.Phys.Rev.Lett.2001. 87.203402.Schmidt,M.;Donges,J.;Hippler,Th.:Haberland,H. the temperature at which C has a peak should be called the Phys.Reu.Let.2003,90.103401. melting temperature since the majority of the system can still (31)Breaux,G.A.:Benirschke,R.C.:Sugai,T.:Kinnear,B.S.:Jarrold, be in the solid state.In a strict sense,since the transition is M.F.Phrys.Rev.Lett.2003.9/,215508. (32)Breaux,G.A.:Hillman.D.A.:Neal,C.M.;Benirschke,R.C.: gradual,there is no melting point at all.Since clusters and Jarrold,M.F.J.Am.Chem.Soc.2004,126,8628. (33)Lai,S.K.:Lin,W.D.:Wu,K.L.;Li,W.H.;Lee,K.C.J.Chem (40)Zhang,W.;Zhang,F.S.;Zhu,Z.Y.Plrys.Rev.B 2006,74,033412 Phys.2004.121,1487. Zhang,W.;Zhang,F.S.;Zhu,Z.Y.Eur.Phys.J.D 2007,43,97. (34)Werner,R.Eur.Phys.J.B 2005.43,47. Zhang.W.:Zhang.F.S.Zhu,Z.Y.Chin.Phys.Len.2007.24. (35)Breaux,G.A.:Cao.B.:Jarrold,M.F.J.Phys.Chem.B 2005,109, 1915. 16575. (41)Duan,H.M.;Ding,F.;Rosen,A.;Harutyunyan,A.R.;Curtarolo, (36)Breaux.G.A.:Neal.C.M.:Cao,B.:Jarrold,M.F.Phrys.Rev.Lett. S.;Bolton,K.Chem.Phys.2007,333,57. 2005,94,173401. (42)Neal,C.M.;Starace,A.K.:Jarrold,M.F.J.Am.Soc.Mass Spectrom. (37)de Bas,B.S.;Ford,M.J.;Cortie,M.B.J.Phys.:Condens.Matter 2007.18.74. 2006.18.55. (43)Neal,C.M.:Starace,A.K.:Jarrold,M.F.;Joshi,K.:Krishnamurty. (38)Joshi,K.;Krishnamurty,S.;Kanhere,D.G.Phys.Rev.Lett.2006, S.:Kanhere,D.G.J.Phys.Chem.C2007,111,17788. 96,135703. (44)Neal,C.M.:Atarace,A.K.;Jarrold,M.F.Phys.Rev.B 2007,76. (39)Noya,E.G.:Doye,J.P.K.:Calvo.F.Plrys.Rev.B 2006.73,125407. 54113. J.AM.CHEM.SOC.VOL.130.NO.38.2008 12699under equilibrium conditions usually occurs in a very narrow temperature and pressure range (spontaneously). A small change in temperature or pressure completely changes the phase from one to the other. Thus, the change of phase can be characterized by a transition temperature Ttran. However, for clusters and nanoparticles ranging in size from several atoms to thousands of atoms, the transition from one equilibrium phase to another equilibrium phase occurs gradually in a wider temperature range.6,11,12,22,23 Within this range the two phases are in equilibrium with each other. Therefore, the phase change in finite systems has to be characterized by two temperatures, T1 and T2 with T2 > T1. 8-10,12 Below T1, the amount of phase 2 is negligible, while above T2, the amount of phase 1 is negligible. For a solid-liquid transition, T1 is the freezing temperature Tf and T2 is the melting temperature Tm. Between the two temperatures is the solid-liquid coexistence region.14-19 For macroscopic systems under equilibrium conditions, Tf ) Tm. 8,10,20,21 Experimentally, one convenient way to study a melting transition is to measure the caloric curve (energy as a function of temperature) of the system.13 The heat capacity is the derivative of the caloric curve. Caloric curves have been used to study the melting of clusters and nanoparticles,6,13,24-44 both experimentally and theoretically, as well as bulk materials. For some cases, the heat capacity curve has a sharp peak, but for others it does not.26,32,35,36,38,42-44 Usually, as in macroscopic systems,21 the former case has been called a first-order melting transition while the latter has often been called a second-order melting transition,35 although there are also second-order phase transitions of other kinds in bulk materials. The temperature at which the heat capacity curve has a peak or maximum will be called the peak temperature (Tp) of the heat capacity. Although the melting temperature is usually taken as this peak temperature, this is not necessarily a valid procedure for finite systems. Consider a model system with only two states, both nondegenerate, which may be two electronic states or two isomers in equilibrium with each other; the partition function of the system is Q ) 1 + e -∆ε⁄kBT (1) where ∆ε is the energy gap between the two states. Then the heat capacity of the system is C ) ∆ε 2 ⁄ kBT2 (e ∆ε⁄2kBT + e -∆ε⁄2kBT ) 2 (2) Plots of C vs T with two different values of ∆ε are depicted in Figure 1. Since the two states involved can be any two states, not necessarily a liquid and a solid state, it is clear that observing a peak in the C curve is not enough to indicate a melting transition. It may just result from equilibrium between two electronic states or two structural isomers with different energies. Moreover, it is easy to show that at Tp the population of the higher energy state is just 13% (e-2 /(1 + e-2 )). Therefore, even if one can call this a melting transition, it is questionable whether the temperature at which C has a peak should be called the melting temperature since the majority of the system can still be in the solid state. In a strict sense, since the transition is gradual, there is no melting point at all. Since clusters and (14) Vichare, A.; Kanhere, D. G. J. Phys: Condens. Matter 1998, 10, 3309. (15) Cleveland, C. L.; Luedtke, W. D.; Landman, U. Phys. ReV. B 1999, 60, 5065. (16) Pochon, S.; MacDonald, K. F.; Knize, R. J.; Zheludev, N. I. Phys. ReV. Lett. 2004, 92, 145702. (17) Schebarchov, D.; Hendy, S. C. J. Chem. Phys. 2006, 123, 104701. (18) Schebarchov, D.; Hendy, S. C. Phys. ReV. B 2006, 73, 121402(R) (19) Alavi, S.; Thompson, D. L. J. Phys. Chem. A 2006, 110, 1518. (20) Atkins, P.; Paula, J. D. Atkins’ Physical Chemistry, 7th ed.; Oxford University Press: New York, 2002; p 135. (21) Berry, R. S.; Rice, S. A.; Ross, J. Physical Chemistry, 2nd ed.; Topics in Physical Chemistry Series 12; Oxford University Press: New York, 2000; pp 397,658. See also p 347. (22) Sebetci, A.; Gu¨venc, Z. B.; Ko¨kten, H. Comput. Mater. Sci. 2006, 35, 152. (23) Rodumer, E. Chem. Soc. ReV. 2006, 35, 583. (24) Rey, C.; Gallego, L. J.; Garcı´a-Rodeja, J.; Alonso, J. A.; In˜iguez, M. P. Phys. ReV. B 1993, 48, 8253. (25) Nayak, S. K.; Khanna, S. N.; Rao, B. K.; Jena, P. J. Phys.: Condens. Matter 1998, 10, 10853. (26) Schmidt, M.; Kusche, R.; Kronmu¨ler, W.; von Issendorff, B.; Haberland, H. Phys. ReV. Lett. 1997, 79, 99. Schmidt, M.; Kusche, R.; von Issendorff, B.; Haberland, H. Nature 1998, 393, 238. (27) Sun, D. Y.; Gong, X. G. Phys. ReV. B 1998, 57, 4730. (28) Efremov, M. Yu.; Schiettekatte, F.; Zhang, M.; Olson, E. A.; Kwan, A. T.; Berry, R. S.; Allen, L. H. Phys. ReV. Lett. 2000, 85, 3560. (29) Jellinek, J.; Goldberg, A. J. Chem. Phys. 2000, 113, 2570. (30) Schmidt, M.; Hippler, Th.; Donges, J.; Kronmu¨ller, W.; von Issendorff, B.; Haberland, H.; Labastie, P. Phys. ReV. Lett. 2001, 87, 203402. Schmidt, M.; Donges, J.; Hippler, Th.; Haberland, H. Phys. ReV. Lett. 2003, 90, 103401. (31) Breaux, G. A.; Benirschke, R. C.; Sugai, T.; Kinnear, B. S.; Jarrold, M. F. Phys. ReV. Lett. 2003, 91, 215508. (32) Breaux, G. A.; Hillman, D. A.; Neal, C. M.; Benirschke, R. C.; Jarrold, M. F. J. Am. Chem. Soc. 2004, 126, 8628. (33) Lai, S. K.; Lin, W. D.; Wu, K. L.; Li, W. H.; Lee, K. C. J. Chem. Phys. 2004, 121, 1487. (34) Werner, R. Eur. Phys. J. B 2005, 43, 47. (35) Breaux, G. A.; Cao, B.; Jarrold, M. F. J. Phys. Chem. B 2005, 109, 16575. (36) Breaux, G. A.; Neal, C. M.; Cao, B.; Jarrold, M. F. Phys. ReV. Lett. 2005, 94, 173401. (37) de Bas, B. S.; Ford, M. J.; Cortie, M. B. J. Phys.: Condens. Matter 2006, 18, 55. (38) Joshi, K.; Krishnamurty, S.; Kanhere, D. G. Phys. ReV. Lett. 2006, 96, 135703. (39) Noya, E. G.; Doye, J. P. K.; Calvo, F. Phys. ReV. B 2006, 73, 125407. (40) Zhang, W.; Zhang, F. S.; Zhu, Z. Y. Phys. ReV. B 2006, 74, 033412. Zhang, W.; Zhang, F. S.; Zhu, Z. Y. Eur. Phys. J. D 2007, 43, 97. Zhang, W.; Zhang, F. S.; Zhu, Z. Y. Chin. Phys. Lett. 2007, 24, 1915. (41) Duan, H. M.; Ding, F.; Rosen, A.; Harutyunyan, A. R.; Curtarolo, S.; Bolton, K. Chem. Phys. 2007, 333, 57. (42) Neal, C. M.; Starace, A. K.; Jarrold, M. F. J. Am. Soc. Mass Spectrom. 2007, 18, 74. (43) Neal, C. M.; Starace, A. K.; Jarrold, M. F.; Joshi, K.; Krishnamurty, S.; Kanhere, D. G. J. Phys. Chem. C 2007, 111, 17788. (44) Neal, C. M.; Atarace, A. K.; Jarrold, M. F. Phys. ReV. B 2007, 76, 54113. Figure 1. Heat capacity of a model system with two nondegenerate states. J. AM. CHEM. SOC. 9 VOL. 130, NO. 38, 2008 12699 Nanosolids, Slushes, and Nanoliquids ARTICLES