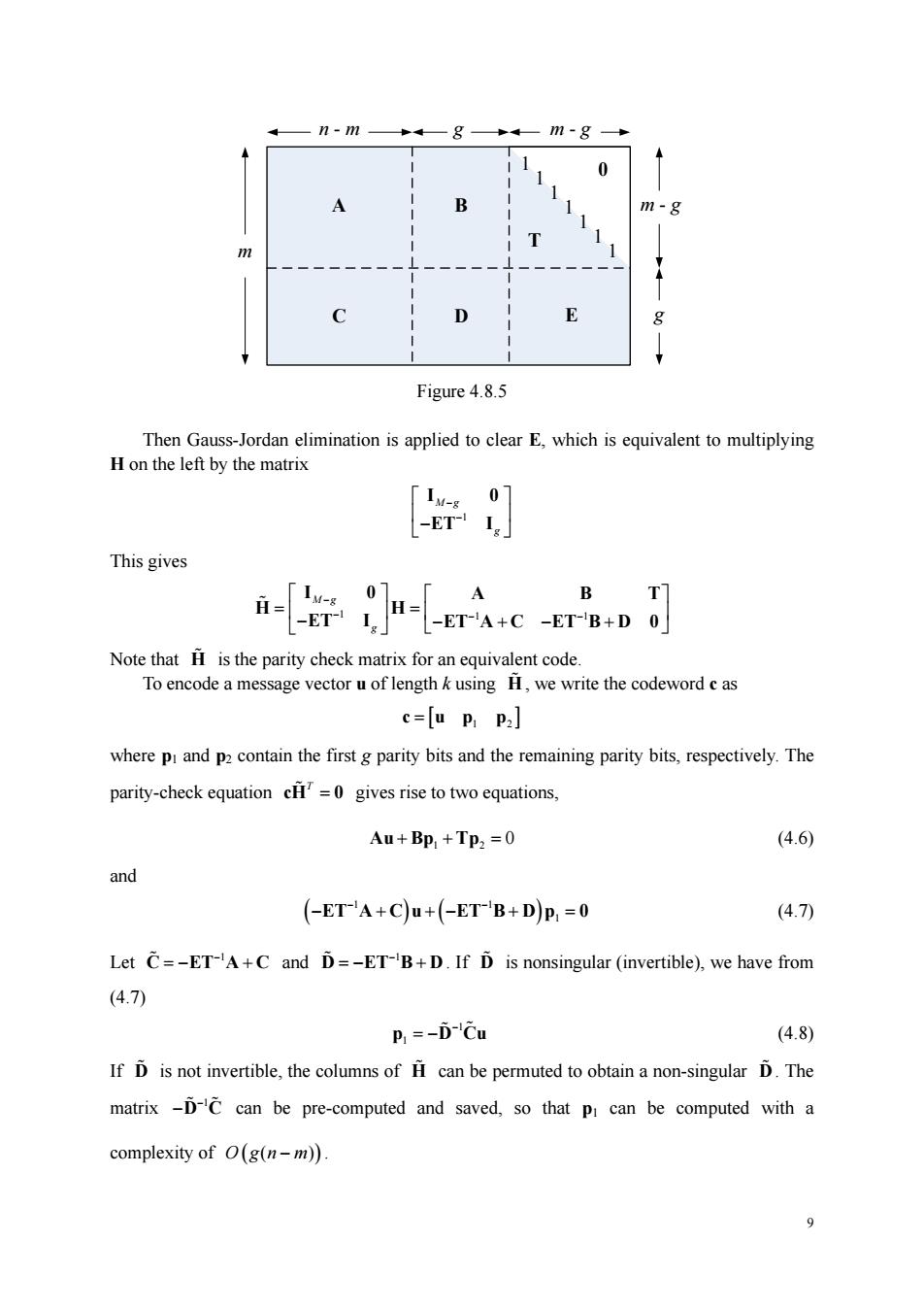
-m-g- Figure 4.8.5 Then Gauss-Jordan elimination is applied to clear E.which is equivalent to multiplying H on the left by the matrix 「1-g0 -ET-I This gives ft-Lu-r 01「A B T] L-ET 1JH-ETA+C -ETB+D 0 Note that is the parity check To encode a message vector u of length k using H,we write the codeword c as c=u P:P2] where p and p contain the first g parity bits and the remaining parity bits,respectively.The parity-check equation c=0gives rise to two equations. Au+Bp:+Tpz=0 (4.6) and (-ET-A+C)u+(-ET-B+D)p,=0 (4.7) Let C=-ET-A+C and D=-ET-B+D.If D is nonsingular (invertible),we have from (4.7) P:=-D-Cu (4.8) If D is not invertible,the columns of H can be permuted to obtain a non-singular D.The matrix -D-C can be pre-computed and saved,so that Pi can be computed with a complexity of (g(n-m)).9 1 0 A 1 1 1 1 1 1 B C D E T n - m g m - g m - g g m Figure 4.8.5 Then Gauss-Jordan elimination is applied to clear E, which is equivalent to multiplying H on the left by the matrix 1 M g g − − ⎡ ⎤ ⎢ ⎥ −⎣ ⎦ I 0 ET I This gives 1 1 1 M g g − − − − ⎡ ⎤ ⎡ ⎤ = = ⎢ ⎥ ⎢ ⎥ ⎣ ⎦ − ⎣− +− + ⎦ I 0 A BT H H ET I ET A C ET B D 0  Note that H is the parity check matrix for an equivalent code. To encode a message vector u of length k using H , we write the codeword c as c up p = [ 1 2 ] where p1 and p2 contain the first g parity bits and the remaining parity bits, respectively. The parity-check equation T cH 0  = gives rise to two equations, 1 2 Au Bp Tp + + = 0 (4.6) and ( ) ( ) 1 1 1 − − − + +− + = ET A C u ET B D p 0 (4.7) Let −1 C ET A C =− +  and −1 D ET B D  =− + . If D is nonsingular (invertible), we have from (4.7) 1 1 − p D Cu = −   (4.8) If D is not invertible, the columns of H can be permuted to obtain a non-singular D . The matrix −1 −D C   can be pre-computed and saved, so that p1 can be computed with a complexity of O gn m ( ) ( ) −