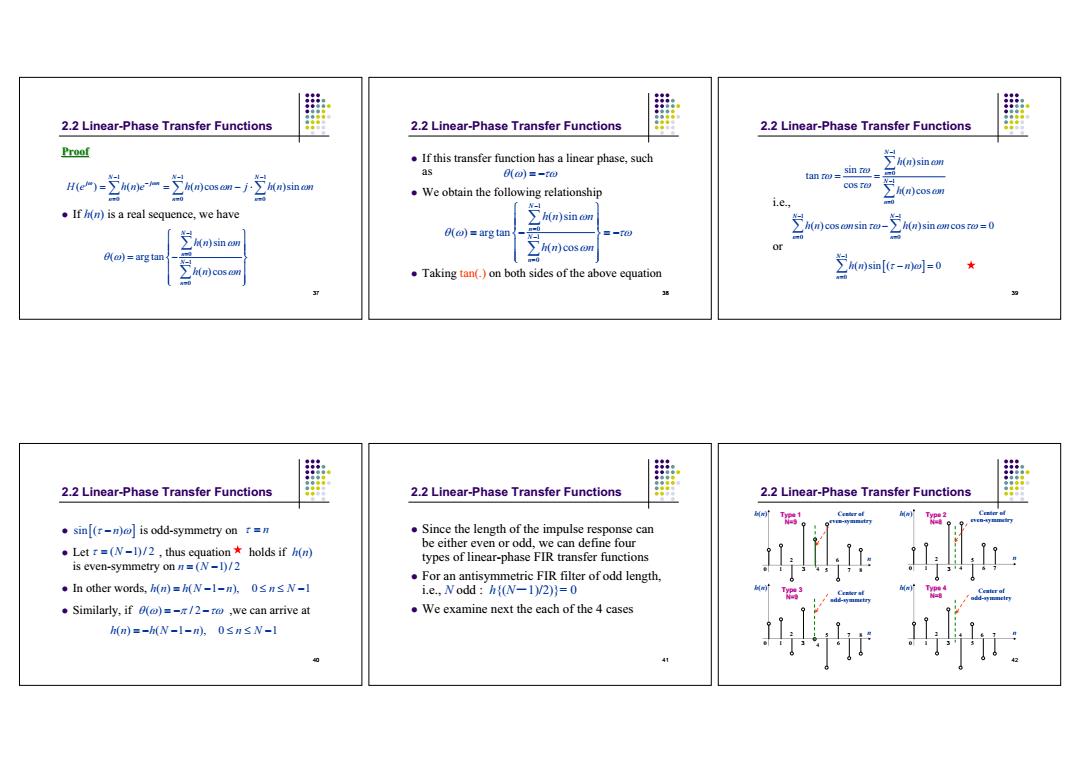
2.2 Linear-Phase Transfer Functions 2.2 Linear-Phase Transfer Functions 2.2 Linear-Phase Transfer Functions Proof If this transfer function has a linear phase,such >h(n)sinc as w)=-t0 He=岁me-分n)cos om-j·分n)sin on tan ro=Sin tw cos ro We obtain the following relationship 风n)cose期 )sin on i.e., If /(m)is a real sequence,we have 分o h(月)sin cn cos ro=0 ()arg tan 》n)sin h(n)coson or (@)arg tan (n)cos Taking tan(.)on both sides of the above equation 岁siml0c-no=0★ 2.2 Linear-Phase Transfer Functions 2.2 Linear-Phase Transfer Functions 2.2 Linear-Phase Transfer Functions .sin[(r-m)]is odd-symmetry on r=m Since the length of the impulse response can be either even or odd,we can define four ·Letr=(N-l)/2,thus equation★holds ifh(m is even-symmetry on n=(N-1)/2 types of linear-phase FIR transfer functions For an antisymmetric FIR filter of odd length, ◆In other words,.hm)=hW-l-n,0sn≤N-l i.e.,Nodd h(N-1)/2))=0 Similarly,if 0(@)=-/2-ro ,we can arrive at We examine next the each of the 4 cases h(n)=-h(N-1-n),0snsN-1 0 r37 2.2 Linear-Phase Transfer Functions Proof If h(n) is a real sequence, we have 11 1 00 0 ( ) ( ) ( )cos ( )sin NN N j jn nn n H e hne hn n j hn n         1 0 1 0 ( )sin ( ) arg tan ( )cos N n N n hn n hn n                    38 2.2 Linear-Phase Transfer Functions If this transfer function has a linear phase, such as We obtain the following relationship Taking tan(.) on both sides of the above equation   ( )   1 0 1 0 ( )sin ( ) arg tan ( )cos N n N n hn n hn n                       39 2.2 Linear-Phase Transfer Functions i.e., or 1 0 1 0 ( )sin sin tan cos ( )cos N n N n hn n hn n          1 1 0 0 ( )cos sin ( )sin cos 0 N N n n hn n hn n           1 0 ( )sin ( ) 0 N n hn n      40 2.2 Linear-Phase Transfer Functions is odd-symmetry on Let , thus equation holds if h(n) is even-symmetry on In other words, Similarly, if ,we can arrive at sin ( )     n   n    ( 1) / 2 N n N   ( 1) / 2 hn hN n n N ( ) ( 1 ), 0 1        ( ) /2   hn hN n n N ( ) ( 1 ), 0 1       41 2.2 Linear-Phase Transfer Functions Since the length of the impulse response can be either even or odd, we can define four types of linear-phase FIR transfer functions For an antisymmetric FIR filter of odd length, i.e., N odd : h{(Nˉ1)/2)}= 0 We examine next the each of the 4 cases 42 2.2 Linear-Phase Transfer Functions h n( ) n 0 1 2 4 5 7 6 3 8 Center of even-symmetry h n( ) n 0 1 2 7 4 5 6 8 3 Center of odd-symmetry h n( ) n 0 1 2 4 7 5 3 6 Center of even-symmetry h n( ) n 0 1 2 4 7 5 6 3 Center of odd-symmetry Type 1 N=9 Type 4 N=8 Type 3 N=9 Type 2 N=8