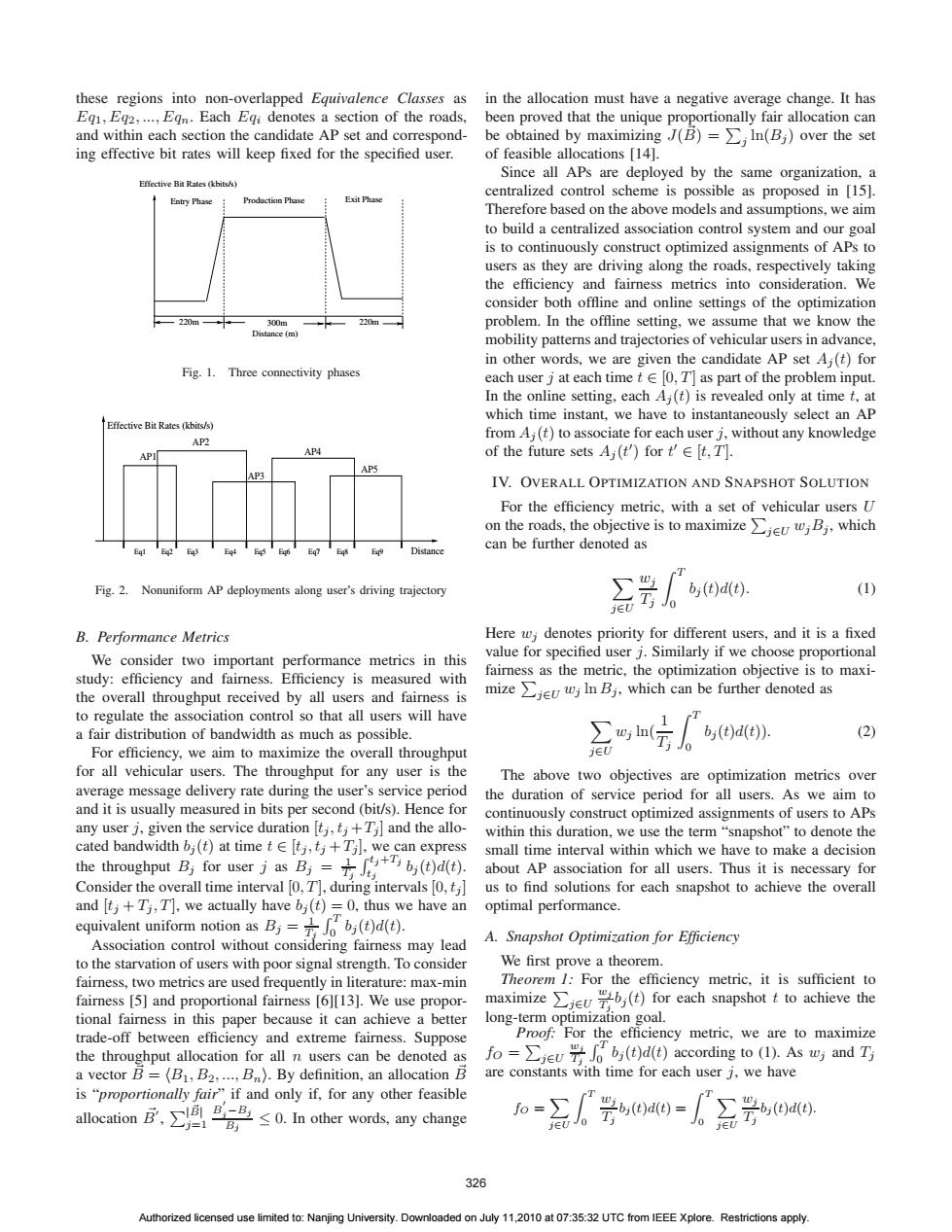
these regions into non-overlapped Equivalence Classes as in the allocation must have a negative average change.It has Eqi,Eg2,...,Eqn.Each Egi denotes a section of the roads,been proved that the unique proportionally fair allocation can and within each section the candidate AP set and correspond-be obtained by maximizing(B)=In(Bj)over the set ing effective bit rates will keep fixed for the specified user. of feasible allocations [141. Since all APs are deployed by the same organization,a Effective Bit Rates(kbits/s) centralized control scheme is possible as proposed in [15]. Entry Phase Production Phase Exit Phase Therefore based on the above models and assumptions,we aim to build a centralized association control system and our goal is to continuously construct optimized assignments of APs to users as they are driving along the roads,respectively taking the efficiency and fairness metrics into consideration.We consider both offline and online settings of the optimization 220m 300m 220a1 problem.In the offline setting,we assume that we know the Distance(m) mobility patterns and trajectories of vehicular users in advance, in other words,we are given the candidate AP set Aj(t)for Fig.1.Three connectivity phases each userj at each time t[0,T]as part of the problem input. In the online setting,each A(t)is revealed only at time t,at which time instant,we have to instantaneously select an AP Effective Bit Rates (kbits/s) AP2 from Aj(t)to associate for each user j,without any knowledge APL AP4 of the future sets Aj(t')for t'[t,T]. AP5 AP3 IV.OVERALL OPTIMIZATION AND SNAPSHOT SOLUTION For the efficiency metric,with a set of vehicular users U on the roads,the objective is to maximize Bj,which E95 Eg6 Distance can be further denoted as Fig.2.Nonuniform AP deployments along user's driving trajectory bi(t)d(t). (1) B.Performance Metrics Here wj denotes priority for different users,and it is a fixed We consider two important performance metrics in this value for specified user j.Similarly if we choose proportional study:efficiency and fairness.Efficiency is measured with fairness as the metric,the optimization objective is to maxi- the overall throughput received by all users and fairness is mizeBj.which can be further denoted as to regulate the association control so that all users will have T a fair distribution of bandwidth as much as possible. bi(t)d(t)). (2) ,0 For efficiency,we aim to maximize the overall throughput jEU for all vehicular users.The throughput for any user is the The above two objectives are optimization metrics over average message delivery rate during the user's service period the duration of service period for all users.As we aim to and it is usually measured in bits per second(bit/s).Hence for continuously construct optimized assignments of users to APs any user j.given the service duration [tj,j+Ti]and the allo- within this duration,we use the term"snapshot"to denote the cated bandwidth bi(t)at time t E [tj,t;+Ti],we can express small time interval within which we have to make a decision the throughput B for users,=士y+b,向dd. about AP association for all users.Thus it is necessary for Consider the overall time interval [0,T].during intervals [0,t]us to find solutions for each snapshot to achieve the overall and [tj+Ti,T],we actually have bi(t)=0.thus we have an optimal performance. equivalent uniform notion as B(td(t). Association control without considering fairness may lead A.Snapshot Optimization for Efficiency to the starvation of users with poor signal strength.To consider We first prove a theorem. fairness,two metrics are used frequently in literature:max-min Theorem /For the efficiency metric,it is sufficient to fairness [5]and proportional fairness [6][13].We use propor- maximize(t)for each snapshot t to achieve the tional fairness in this paper because it can achieve a better long-term optimization goal. trade-off between efficiency and extreme fairness.Suppose Proof:For the efficiency metric,we are to maximize the throughput allocation for all n users can be denoted as fo=∑jeu号0b(t)d(e)according to(I).As wj and Tj a vector B=(B1,B2,...,Bn).By definition,an allocation B are constants with time for each user j,we have is "proportionally fair"if and only if,for any other feasible T allocaion戌，∑A马号≤0 In other ords,ay change fo= Jo jeU 326 Authorized licensed use limited to:Nanjing University.Downloaded on July 11,2010 at 07:35:32 UTC from IEEE Xplore.Restrictions apply.these regions into non-overlapped Equivalence Classes as Eq1,Eq2, ..., Eqn. Each Eqi denotes a section of the roads, and within each section the candidate AP set and correspond￾ing effective bit rates will keep fixed for the specified user. Entry Phase Production Phase Exit Phase Effective Bit Rates (kbits/s) Distance (m) 220m 300m 220m Fig. 1. Three connectivity phases AP2 AP4 AP5 Eq1 Eq2 Eq3 Eq4 Eq5 Eq6 Eq7 Eq8 Eq9 Effective Bit Rates (kbits/s) Distance AP1 AP3 Fig. 2. Nonuniform AP deployments along user’s driving trajectory B. Performance Metrics We consider two important performance metrics in this study: efficiency and fairness. Efficiency is measured with the overall throughput received by all users and fairness is to regulate the association control so that all users will have a fair distribution of bandwidth as much as possible. For efficiency, we aim to maximize the overall throughput for all vehicular users. The throughput for any user is the average message delivery rate during the user’s service period and it is usually measured in bits per second (bit/s). Hence for any user j, given the service duration [tj , tj +Tj] and the allo￾cated bandwidth bj (t) at time t ∈ [tj , tj +Tj], we can express the throughput Bj for user j as Bj = 1 Tj tj+Tj tj bj (t)d(t). Consider the overall time interval [0, T ], during intervals [0, tj] and [tj + Tj , T ], we actually have bj (t)=0, thus we have an equivalent uniform notion as Bj = 1 Tj T 0 bj (t)d(t). Association control without considering fairness may lead to the starvation of users with poor signal strength. To consider fairness, two metrics are used frequently in literature: max-min fairness [5] and proportional fairness [6][13]. We use propor￾tional fairness in this paper because it can achieve a better trade-off between efficiency and extreme fairness. Suppose the throughput allocation for all n users can be denoted as a vector B = B1, B2, ..., Bn. By definition, an allocation B is “proportionally fair” if and only if, for any other feasible allocation B , |B | j=1 B j−Bj Bj ≤ 0. In other words, any change in the allocation must have a negative average change. It has been proved that the unique proportionally fair allocation can be obtained by maximizing J(B ) = j ln(Bj ) over the set of feasible allocations [14]. Since all APs are deployed by the same organization, a centralized control scheme is possible as proposed in [15]. Therefore based on the above models and assumptions, we aim to build a centralized association control system and our goal is to continuously construct optimized assignments of APs to users as they are driving along the roads, respectively taking the efficiency and fairness metrics into consideration. We consider both offline and online settings of the optimization problem. In the offline setting, we assume that we know the mobility patterns and trajectories of vehicular users in advance, in other words, we are given the candidate AP set Aj (t) for each user j at each time t ∈ [0, T ] as part of the problem input. In the online setting, each Aj (t) is revealed only at time t, at which time instant, we have to instantaneously select an AP from Aj (t) to associate for each user j, without any knowledge of the future sets Aj (t ) for t ∈ [t, T ]. IV. OVERALL OPTIMIZATION AND SNAPSHOT SOLUTION For the efficiency metric, with a set of vehicular users U on the roads, the objective is to maximize j∈U wjBj , which can be further denoted as  j∈U wj Tj  T 0 bj (t)d(t). (1) Here wj denotes priority for different users, and it is a fixed value for specified user j. Similarly if we choose proportional fairness as the metric, the optimization objective is to maxi￾mize j∈U wj ln Bj , which can be further denoted as  j∈U wj ln( 1 Tj  T 0 bj (t)d(t)). (2) The above two objectives are optimization metrics over the duration of service period for all users. As we aim to continuously construct optimized assignments of users to APs within this duration, we use the term “snapshot” to denote the small time interval within which we have to make a decision about AP association for all users. Thus it is necessary for us to find solutions for each snapshot to achieve the overall optimal performance. A. Snapshot Optimization for Efficiency We first prove a theorem. Theorem 1: For the efficiency metric, it is sufficient to maximize j∈U wj Tj bj (t) for each snapshot t to achieve the long-term optimization goal. Proof: For the efficiency metric, we are to maximize fO = j∈U wj Tj T 0 bj (t)d(t) according to (1). As wj and Tj are constants with time for each user j, we have fO =  j∈U  T 0 wj Tj bj (t)d(t) =  T 0  j∈U wj Tj bj (t)d(t). 326 Authorized licensed use limited to: Nanjing University. Downloaded on July 11,2010 at 07:35:32 UTC from IEEE Xplore. Restrictions apply.