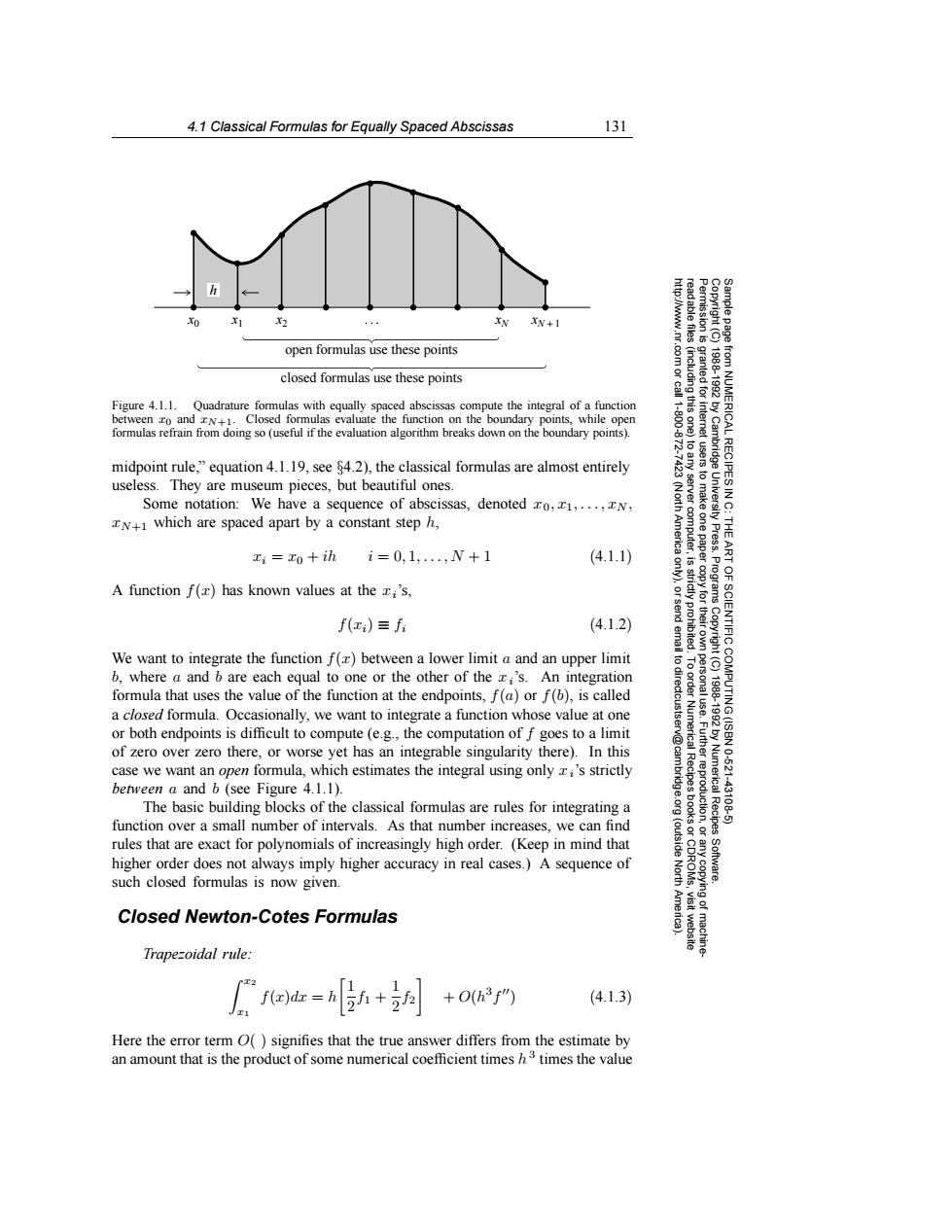
4.1 Classical Formulas for Equally Spaced Abscissas 131 2 4 XN+1 open formulas use these points 83g closed formulas use these points from NUMERICAL RECIPESI 19881992 Figure 4.1.1.Quadrature formulas with equally spaced abscissas compute the integral of a function between ro and N+1.Closed formulas evaluate the function on the boundary points,while open 1.200 formulas refrain from doing so(useful if the evaluation algorithm breaks down on the boundary points). midpoint rule,"equation 4.1.19,see 84.2),the classical formulas are almost entirely useless.They are museum pieces,but beautiful ones. Some notation:We have a sequence of abscissas,denoted xo,x1,...,N, xN+1 which are spaced apart by a constant step h, x=x0+ihi=0,1,,N+1 (4.1.1) 手ge 令 Press. A function f(z)has known values at the zi's, 9 f(x)三f (4.1.2) IENTIFIC We want to integrate the function f()between a lower limit a and an upper limit 6 b,where a and b are each equal to one or the other of the xi's.An integration formula that uses the value of the function at the endpoints,f(a)or f(b),is called a closed formula.Occasionally,we want to integrate a function whose value at one or both endpoints is difficult to compute (e.g.,the computation of f goes to a limit of zero over zero there,or worse yet has an integrable singularity there).In this case we want an open formula,which estimates the integral using only i's strictly 10621 between a and b (see Figure 4.1.1). The basic building blocks of the classical formulas are rules for integrating a Fuurggoglrion 43106 function over a small number of intervals.As that number increases,we can find rules that are exact for polynomials of increasingly high order.(Keep in mind that (outside higher order does not always imply higher accuracy in real cases.)A sequence of Software. such closed formulas is now given. North 6 Closed Newton-Cotes Formulas Trapezoidal rule: f(x)dr= +2 +0h3f" (4.1.3) /x1 Here the error term O()signifies that the true answer differs from the estimate by an amount that is the product of some numerical coefficient times h3 times the value4.1 Classical Formulas for Equally Spaced Abscissas 131 Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). x0 xN xN + 1 open formulas use these points closed formulas use these points x1 x2 h Figure 4.1.1. Quadrature formulas with equally spaced abscissas compute the integral of a function between x0 and xN+1. Closed formulas evaluate the function on the boundary points, while open formulas refrain from doing so (useful if the evaluation algorithm breaks down on the boundary points). midpoint rule,” equation 4.1.19, see §4.2), the classical formulas are almost entirely useless. They are museum pieces, but beautiful ones. Some notation: We have a sequence of abscissas, denoted x0, x1,...,xN , xN+1 which are spaced apart by a constant step h, xi = x0 + ih i = 0, 1,...,N +1 (4.1.1) A function f(x) has known values at the xi’s, f(xi) ≡ fi (4.1.2) We want to integrate the function f(x) between a lower limit a and an upper limit b, where a and b are each equal to one or the other of the xi’s. An integration formula that uses the value of the function at the endpoints, f(a) or f(b), is called a closed formula. Occasionally, we want to integrate a function whose value at one or both endpoints is difficult to compute (e.g., the computation of f goes to a limit of zero over zero there, or worse yet has an integrable singularity there). In this case we want an open formula, which estimates the integral using only xi’s strictly between a and b (see Figure 4.1.1). The basic building blocks of the classical formulas are rules for integrating a function over a small number of intervals. As that number increases, we can find rules that are exact for polynomials of increasingly high order. (Keep in mind that higher order does not always imply higher accuracy in real cases.) A sequence of such closed formulas is now given. Closed Newton-Cotes Formulas Trapezoidal rule:
x2 x1 f(x)dx = h 1 2 f1 + 1 2 f2 + O(h3f

) (4.1.3) Here the error term O( ) signifies that the true answer differs from the estimate by an amount that is the product of some numerical coefficient times h3 times the value