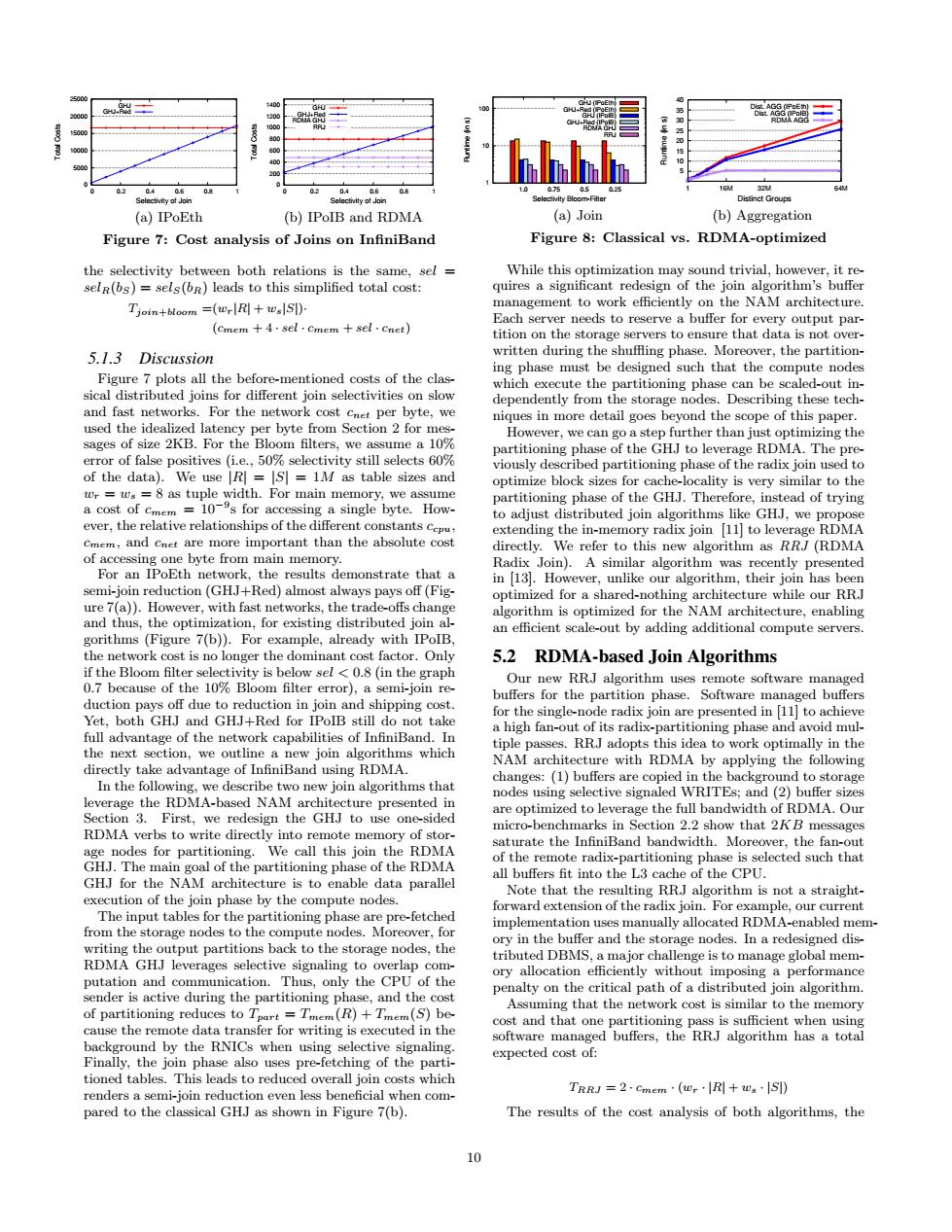
(a)IPoEth (b)IPoIB and RDMA (a)Joir (b)Aggregation Figure 7:Cost analysis of Joins on InfiniBand Figure 8:Classical vs.RDMA-optimized htmraieaaedaio gement to e NAM architectur tition on the re that data 5 13 Discussion t be designed such that the ned costs of the clas sica from Section 2 for ni the byte inmore detail gos beyond the sope of this paper. 50%selectivity still se ts609 partition of the RDMA The optimize block si es for ca cality is very similar to th How GHJ.w g and cnet a of. he result demonstrate vas their te optim ed for ure while our RRJ 5.2 RDMA-based Join Algorithms 10%B ote software m not this id ork opt mally in th M ar ure with RDM (1)b nodes u electiesignal 2 micro-benchma rks in Xntoeno P of the is selected such that the NAM of the l e by the pute nodes not a straight nodces.aprefietdl o ard to the c fo lons bac n t odes,the ged dis tation and ory perfo io on the CP to the of partitioning reduce to 7 =T )+T (S)b that the netwo k cost is simila t on ctiv pre expected cost TRRI=2.cmm(+w-Sl) en com The results of the analysis of both algorithms,the0 5000 10000 15000 20000 25000 0 0.2 0.4 0.6 0.8 1 Total Costs Selectivity of Join GHJ GHJ+Red (a) IPoEth 0 200 400 600 800 1000 1200 1400 0 0.2 0.4 0.6 0.8 1 Total Costs Selectivity of Join GHJ GHJ+Red RDMA GHJ RRJ (b) IPoIB and RDMA Figure 7: Cost analysis of Joins on InfiniBand the selectivity between both relations is the same, sel = selR(bS) = selS(bR) leads to this simplified total cost: Tjoin+bloom =(wr|R| + ws|S|)· (cmem + 4 · sel · cmem + sel · cnet) 5.1.3 Discussion Figure 7 plots all the before-mentioned costs of the clas￾sical distributed joins for different join selectivities on slow and fast networks. For the network cost cnet per byte, we used the idealized latency per byte from Section 2 for mes￾sages of size 2KB. For the Bloom filters, we assume a 10% error of false positives (i.e., 50% selectivity still selects 60% of the data). We use |R| = |S| = 1M as table sizes and wr = ws = 8 as tuple width. For main memory, we assume a cost of cmem = 10−9 s for accessing a single byte. How￾ever, the relative relationships of the different constants ccpu, cmem, and cnet are more important than the absolute cost of accessing one byte from main memory. For an IPoEth network, the results demonstrate that a semi-join reduction (GHJ+Red) almost always pays off (Fig￾ure 7(a)). However, with fast networks, the trade-offs change and thus, the optimization, for existing distributed join al￾gorithms (Figure 7(b)). For example, already with IPoIB, the network cost is no longer the dominant cost factor. Only if the Bloom filter selectivity is below sel < 0.8 (in the graph 0.7 because of the 10% Bloom filter error), a semi-join re￾duction pays off due to reduction in join and shipping cost. Yet, both GHJ and GHJ+Red for IPoIB still do not take full advantage of the network capabilities of InfiniBand. In the next section, we outline a new join algorithms which directly take advantage of InfiniBand using RDMA. In the following, we describe two new join algorithms that leverage the RDMA-based NAM architecture presented in Section 3. First, we redesign the GHJ to use one-sided RDMA verbs to write directly into remote memory of stor￾age nodes for partitioning. We call this join the RDMA GHJ. The main goal of the partitioning phase of the RDMA GHJ for the NAM architecture is to enable data parallel execution of the join phase by the compute nodes. The input tables for the partitioning phase are pre-fetched from the storage nodes to the compute nodes. Moreover, for writing the output partitions back to the storage nodes, the RDMA GHJ leverages selective signaling to overlap com￾putation and communication. Thus, only the CPU of the sender is active during the partitioning phase, and the cost of partitioning reduces to Tpart = Tmem(R) + Tmem(S) be￾cause the remote data transfer for writing is executed in the background by the RNICs when using selective signaling. Finally, the join phase also uses pre-fetching of the parti￾tioned tables. This leads to reduced overall join costs which renders a semi-join reduction even less beneficial when com￾pared to the classical GHJ as shown in Figure 7(b). 1 10 100 1.0 0.75 0.5 0.25 Runtime (in s) Selectivity Bloom-Filter GHJ (IPoEth) GHJ+Red (IPoEth) GHJ (IPoIB) GHJ+Red (IPoIB) RDMA GHJ RRJ (a) Join 5 10 15 20 25 30 35 40 1 16M 32M 64M Runtime (in s) Distinct Groups Dist. AGG (IPoEth) Dist. AGG (IPoIB) RDMA AGG (b) Aggregation Figure 8: Classical vs. RDMA-optimized While this optimization may sound trivial, however, it re￾quires a significant redesign of the join algorithm’s buffer management to work efficiently on the NAM architecture. Each server needs to reserve a buffer for every output par￾tition on the storage servers to ensure that data is not over￾written during the shuffling phase. Moreover, the partition￾ing phase must be designed such that the compute nodes which execute the partitioning phase can be scaled-out in￾dependently from the storage nodes. Describing these tech￾niques in more detail goes beyond the scope of this paper. However, we can go a step further than just optimizing the partitioning phase of the GHJ to leverage RDMA. The pre￾viously described partitioning phase of the radix join used to optimize block sizes for cache-locality is very similar to the partitioning phase of the GHJ. Therefore, instead of trying to adjust distributed join algorithms like GHJ, we propose extending the in-memory radix join [11] to leverage RDMA directly. We refer to this new algorithm as RRJ (RDMA Radix Join). A similar algorithm was recently presented in [13]. However, unlike our algorithm, their join has been optimized for a shared-nothing architecture while our RRJ algorithm is optimized for the NAM architecture, enabling an efficient scale-out by adding additional compute servers. 5.2 RDMA-based Join Algorithms Our new RRJ algorithm uses remote software managed buffers for the partition phase. Software managed buffers for the single-node radix join are presented in [11] to achieve a high fan-out of its radix-partitioning phase and avoid mul￾tiple passes. RRJ adopts this idea to work optimally in the NAM architecture with RDMA by applying the following changes: (1) buffers are copied in the background to storage nodes using selective signaled WRITEs; and (2) buffer sizes are optimized to leverage the full bandwidth of RDMA. Our micro-benchmarks in Section 2.2 show that 2KB messages saturate the InfiniBand bandwidth. Moreover, the fan-out of the remote radix-partitioning phase is selected such that all buffers fit into the L3 cache of the CPU. Note that the resulting RRJ algorithm is not a straight￾forward extension of the radix join. For example, our current implementation uses manually allocated RDMA-enabled mem￾ory in the buffer and the storage nodes. In a redesigned dis￾tributed DBMS, a major challenge is to manage global mem￾ory allocation efficiently without imposing a performance penalty on the critical path of a distributed join algorithm. Assuming that the network cost is similar to the memory cost and that one partitioning pass is sufficient when using software managed buffers, the RRJ algorithm has a total expected cost of: TRRJ = 2 · cmem · (wr · |R| + ws · |S|) The results of the cost analysis of both algorithms, the 10