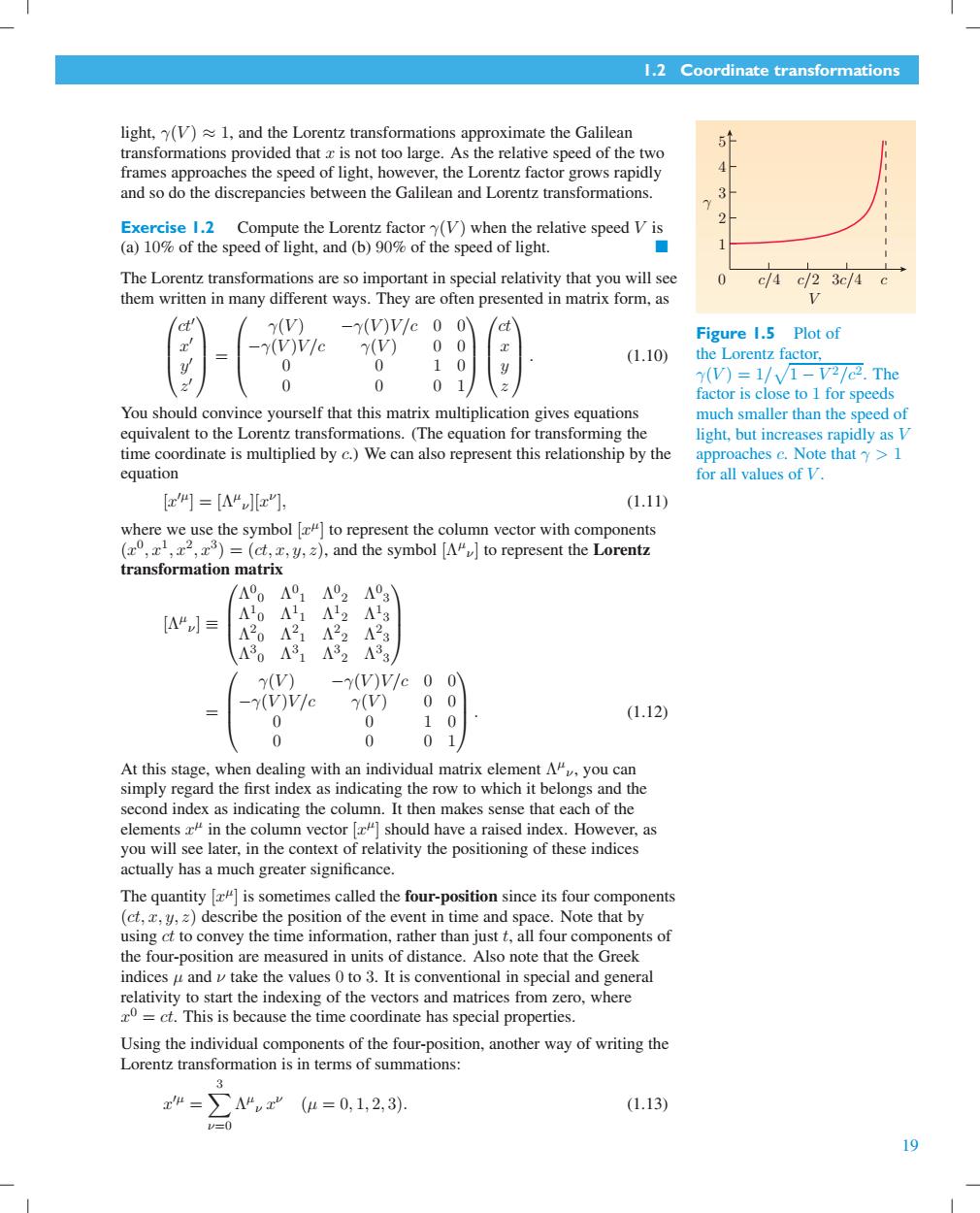
1.2 Coordinate transformations light,(V)1,and the Lorentz transformations approximate the Galilean 51 transformations provided that z is not too large.As the relative speed of the two frames approaches the speed of light,however,the Lorentz factor grows rapidly 4 and so do the discrepancies between the Galilean and Lorentz transformations. 2 3 2 Exercise 1.2 Compute the Lorentz factor y(V)when the relative speed V is (a)10%of the speed of light,and (b)90%of the speed of light. ■ The Lorentz transformations are so important in special relativity that you will see 0 c/4c/23c/4c them written in many different ways.They are often presented in matrix form,as ct' Y(V) -(V)V/e0 0 d Figure 1.5 Plot of (V)V/c (V) 0 0 0 0 0 (1.10) the Lorentz factor, y 0 0 0 Y(V)=1/V1-V2/2.The 2 factor is close to 1 for speeds You should convince yourself that this matrix multiplication gives equations much smaller than the speed of equivalent to the Lorentz transformations.(The equation for transforming the light,but increases rapidly as V time coordinate is multiplied by c.)We can also represent this relationship by the approaches c.Note that >1 equation for all values of V. [z4]=A“a"], (1.11) where we use the symbol [to represent the column vector with components (z0,1,2,3)=(ct,,y,z),and the symbol [AM]to represent the Lorentz transformation matrix A00A01 A02 A03 [A“≡ Λ12Λ13 A201 21A22 423 430A31A32433 Y(V) -(V)V/c 0 0 -y(V)V/c 7(V) 0 0 0 0 10 (1.12) 0 0 0 1 At this stage,when dealing with an individual matrix element Av,you can simply regard the first index as indicating the row to which it belongs and the second index as indicating the column.It then makes sense that each of the elements x#in the column vector [x]should have a raised index.However,as you will see later,in the context of relativity the positioning of these indices actually has a much greater significance. The quantity [#]is sometimes called the four-position since its four components (ct,,y,z)describe the position of the event in time and space.Note that by using ct to convey the time information,rather than just t,all four components of the four-position are measured in units of distance.Also note that the Greek indices u and v take the values 0 to 3.It is conventional in special and general relativity to start the indexing of the vectors and matrices from zero,where 0=ct.This is because the time coordinate has special properties. Using the individual components of the four-position,another way of writing the Lorentz transformation is in terms of summations: 3 x4=>△“x'(4=0,1,2,3) (1.13) =0 191.2 Coordinate transformations light, γ(V ) ≈ 1, and the Lorentz transformations approximate the Galilean transformations provided that x is not too large. As the relative speed of the two frames approaches the speed of light, however, the Lorentz factor grows rapidly and so do the discrepancies between the Galilean and Lorentz transformations. γ 0 1 2 4 3 5 c/4 c/2 3c/4 c V Figure 1.5 Plot of the Lorentz factor, γ(V ) = 1/ - 1 − V 2/c2. The factor is close to 1 for speeds much smaller than the speed of light, but increases rapidly as V approaches c. Note that γ > 1 for all values of V . Exercise 1.2 Compute the Lorentz factor γ(V ) when the relative speed V is (a) 10% of the speed of light, and (b) 90% of the speed of light. ■ The Lorentz transformations are so important in special relativity that you will see them written in many different ways. They are often presented in matrix form, as   ct% x % y % z %   =   γ(V ) −γ(V )V /c 0 0 −γ(V )V /c γ(V ) 0 0 0 0 1 0 0 0 0 1     ct x y z   . (1.10) You should convince yourself that this matrix multiplication gives equations equivalent to the Lorentz transformations. (The equation for transforming the time coordinate is multiplied by c.) We can also represent this relationship by the equation [x %µ ] = [Λµ ν][x ν ], (1.11) where we use the symbol [x µ ] to represent the column vector with components (x 0 , x1 , x2 , x3 ) = (ct, x, y, z), and the symbol [Λµ ν ] to represent the Lorentz transformation matrix [Λµ ν ] ≡   Λ 0 0 Λ 0 1 Λ 0 2 Λ 0 3 Λ 1 0 Λ 1 1 Λ 1 2 Λ 1 3 Λ 2 0 Λ 2 1 Λ 2 2 Λ 2 3 Λ 3 0 Λ 3 1 Λ 3 2 Λ 3 3   =   γ(V ) −γ(V )V /c 0 0 −γ(V )V /c γ(V ) 0 0 0 0 1 0 0 0 0 1   . (1.12) At this stage, when dealing with an individual matrix element Λ µ ν , you can simply regard the first index as indicating the row to which it belongs and the second index as indicating the column. It then makes sense that each of the elements x µ in the column vector [x µ ] should havearaised index. However, as you will see later, in the context of relativity the positioning of these indices actually has a much greater significance. The quantity [x µ ] is sometimes called the four-position since its four components (ct, x, y, z) describe the position of the event in time and space. Note that by using ct to convey the time information, rather than just t, all four components of the four-position are measured in units of distance. Also note that the Greek indices µ and ν take the values 0 to 3. It is conventional in special and general relativity to start the indexing of the vectors and matrices from zero, where x 0 = ct. This is because the time coordinate has special properties. Using the individual components of the four-position, another way of writing the Lorentz transformation is in terms of summations: x %µ = A 3 ν=0 Λ µ ν x ν (µ = 0, 1, 2, 3). (1.13) 19