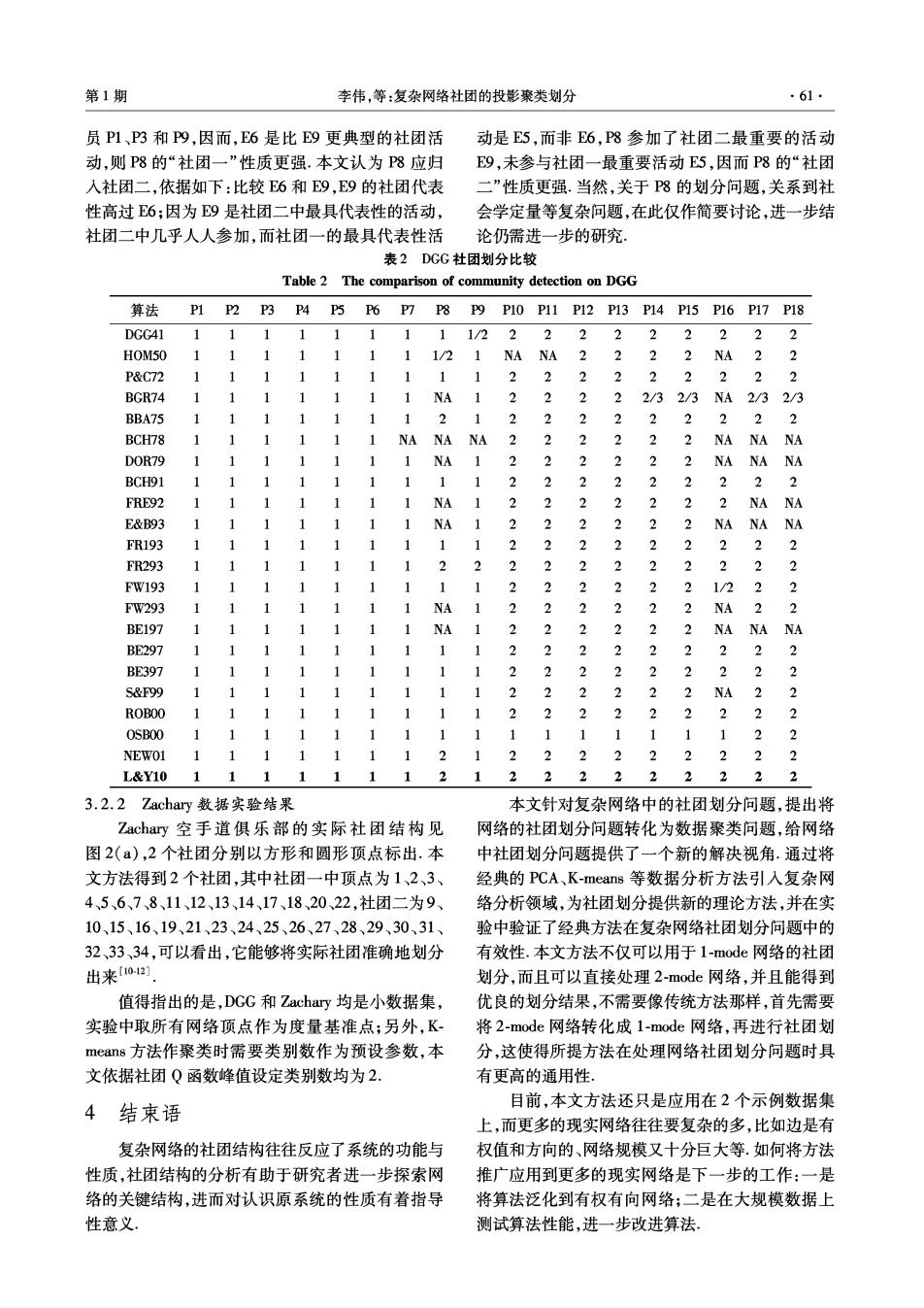
第1期 李伟，等：复杂网络社团的投影聚类划分 61… 员P1、P3和P9,因而，E6是比E9更典型的社团活 动是E5,而非6，P8参加了社团二最重要的活动 动，则P8的“社团一”性质更强.本文认为P8应归 E9,未参与社团一最重要活动E5,因而P8的“社团 入社团二，依据如下：比较E6和E9,E9的社团代表 二”性质更强.当然，关于P8的划分问题，关系到社 性高过E6;因为9是社团二中最具代表性的活动， 会学定量等复杂问题，在此仅作简要讨论，进一步结 社团二中几乎人人参加，而社团一的最具代表性活 论仍需进一步的研究， 表2DGG社团划分比较 Table 2 The comparison of community detection on DGG 算法 P1P2P3P4P5P6P7P8P9P10P11P12P13P14P15P16P17P18 DGG41 111 1111/2222222 222 HOM50 1 1 11/2 1 NA NA 2 2 2 2 NA 22 P&C72 1 1 2 2 2 2 2 BGR74 1 NA 2 2 2 2/32/3NA2/32/3 BBA75 1 1 2 2 2 2 2 2 2 2 2 BCH78 1 1 NA NA 2 2 2 2 2 2 NA D0R79 1 1 2 2 NA NA NA BCH91 1 1 2 2 2 2 FRE92 1 2 NA NA E&B93 nAnA Na FR193 1 2 2 2 FR293 1 2 2 2 2 FW193 1 2 2 1/2 2 FW293 1 1 NA 2 2 BE197 1 1 NA 2 NA NA NA BE297 1 1 2 BF397 2 2 2 2 2 S&F99 1 1 1 2 2 2 2 NA 2 2 ROBOO 1 1 1 2 2 2 2 2 2 2 2 OSBOO 1 1 2 2 NEWO1 1 1 1 1 1 2 1 2 2 2 2 2 2 2 2 2 L&Y10 1 1 1 1 2 1 2 2 2 2 2 2 2 3.2.2 Zachary数据实验结果 本文针对复杂网络中的社团划分问题，提出将 Zachary空手道俱乐部的实际社团结构见 网络的社团划分问题转化为数据聚类问题，给网络 图2(a),2个社团分别以方形和圆形顶点标出.本 中社团划分问题提供了一个新的解决视角.通过将 文方法得到2个社团，其中社团一中顶点为1、2、3、 经典的PCA、K-means等数据分析方法引入复杂网 4、5、6、7、8、11、12、13、14、17、18、20、22,社团二为9、 络分析领域，为社团划分提供新的理论方法，并在实 10、15、16、19、21、23、24、25、26、27、28、29、30、31、 验中验证了经典方法在复杂网络社团划分问题中的 32、33、34,可以看出，它能够将实际社团准确地划分 有效性.本文方法不仅可以用于1-mode网络的社团 出来[10-121 划分，而且可以直接处理2-mode网络，并且能得到 值得指出的是，DGG和Zachary均是小数据集， 优良的划分结果，不需要像传统方法那样，首先需要 实验中取所有网络顶点作为度量基准点；另外，K- 将2-mode网络转化成1-mode网络，再进行社团划 means方法作聚类时需要类别数作为预设参数，本 分，这使得所提方法在处理网络社团划分问题时具 文依据社团Q函数峰值设定类别数均为2. 有更高的通用性 目前，本文方法还只是应用在2个示例数据集 4结束语 上，而更多的现实网络往往要复杂的多，比如边是有 复杂网络的社团结构往往反应了系统的功能与 权值和方向的、网络规模又十分巨大等.如何将方法 性质，社团结构的分析有助于研究者进一步探索网 推广应用到更多的现实网络是下一步的工作：一是 络的关键结构，进而对认识原系统的性质有着指导 将算法泛化到有权有向网络；二是在大规模数据上 性意义 测试算法性能，进一步改进算法