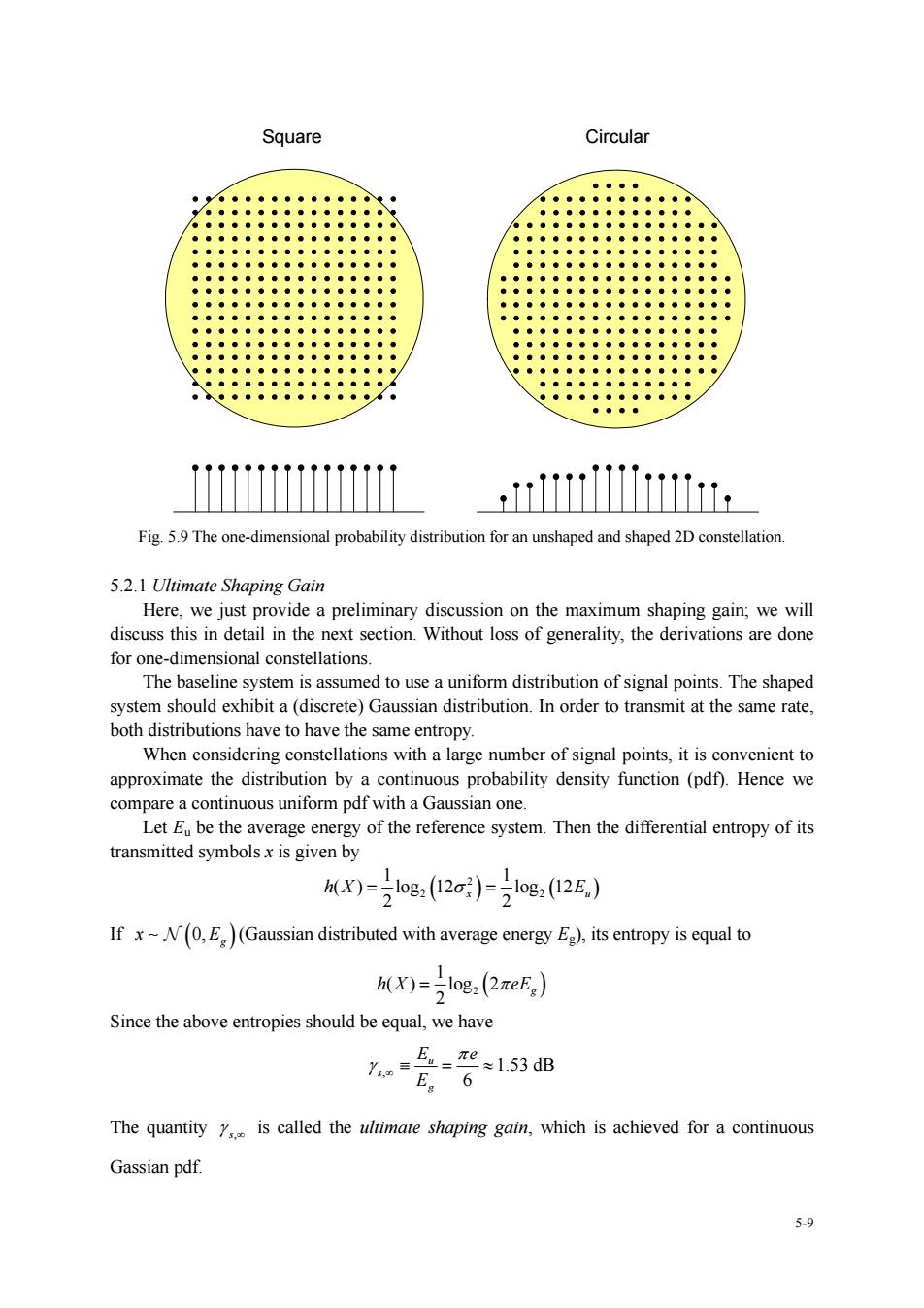
Square Circular Fig.59The one-dimensional probability distribution for an unshaped and shaped 2D constellation 5.2.1 Ultimate Shaping Gain Here,we just provide a preliminary discussion on the maximum shaping gain,we will discuss this in detail in the next section.Without loss of generality,the derivations are done for one-dimensional constellations ystem is ass med to use auniform distribution of signal points.The shaped ystemshou(disrete) both distributions have to have the same entropy. When considering constellations with a large number of signal points,it is convenient to approximate the distribution by a continuous probability density function(pdf).Hence we ompare a continuous uniform pdf with a Gaussian one. Let Ebe the verage energy of the reference system.Then the differential entropy of its transmitted symbolsx is given by MX)=g:2c)=g:2E) If x-N(0,E)(Gaussian distributed with average energy E).its entropy is equal to h(X)=log2(2πeE) Since the above entropies should be equal,we have E2-形=1.53dB 6 The quantity is called the ultimate shaping gain,which is achieved for a continuous Gassian pdf. 5.9 5-9 Square Circular Fig. 5.9 The one-dimensional probability distribution for an unshaped and shaped 2D constellation. 5.2.1 Ultimate Shaping Gain Here, we just provide a preliminary discussion on the maximum shaping gain; we will discuss this in detail in the next section. Without loss of generality, the derivations are done for one-dimensional constellations. The baseline system is assumed to use a uniform distribution of signal points. The shaped system should exhibit a (discrete) Gaussian distribution. In order to transmit at the same rate, both distributions have to have the same entropy. When considering constellations with a large number of signal points, it is convenient to approximate the distribution by a continuous probability density function (pdf). Hence we compare a continuous uniform pdf with a Gaussian one. Let Eu be the average energy of the reference system. Then the differential entropy of its transmitted symbols x is given by ( ) ( ) 2 2 2 1 1 ( ) log 12 log 12 2 2 x u hX E = = σ If ( ) 0, g x ∼ N E (Gaussian distributed with average energy Eg), its entropy is equal to 2 ( ) 1 ( ) log 2 2 g h X eE = π Since the above entropies should be equal, we have , 1.53 dB 6 u s g E e E π γ ∞ ≡=≈ The quantity s, γ ∞ is called the ultimate shaping gain, which is achieved for a continuous Gassian pdf