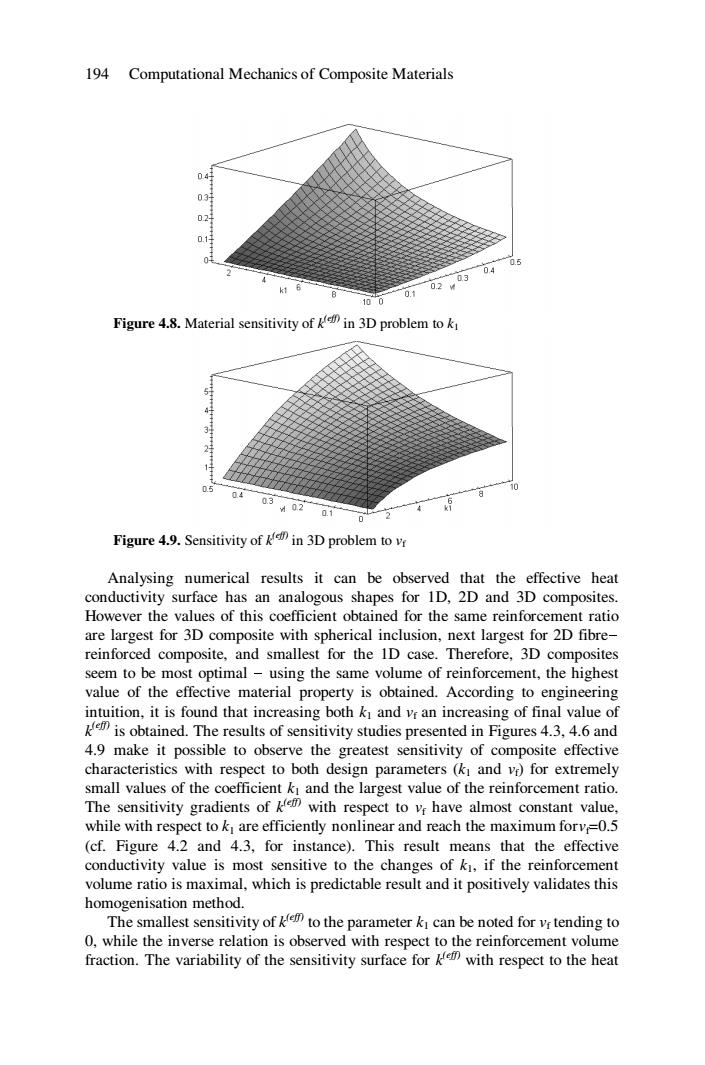
194 Computational Mechanics of Composite Materials 04时 03 02 0.1 0 0.5 04 0.1 0203 100 Figure 4.8.Material sensitivity of in 3D problem to k 2 1 0.5 04 0.3 02 0.1 0 Figure 4.9.Sensitivity of in 3D problem to Analysing numerical results it can be observed that the effective heat conductivity surface has an analogous shapes for 1D,2D and 3D composites. However the values of this coefficient obtained for the same reinforcement ratio are largest for 3D composite with spherical inclusion,next largest for 2D fibre- reinforced composite,and smallest for the 1D case.Therefore,3D composites seem to be most optimal-using the same volume of reinforcement,the highest value of the effective material property is obtained.According to engineering intuition,it is found that increasing both k and vr an increasing of final value of is obtained.The results of sensitivity studies presented in Figures 4.3.4.6 and 4.9 make it possible to observe the greatest sensitivity of composite effective characteristics with respect to both design parameters(k and vr)for extremely small values of the coefficient ki and the largest value of the reinforcement ratio. The sensitivity gradients ofkm with respect to vr have almost constant value, while with respect to k are efficiently nonlinear and reach the maximum forv=0.5 (cf.Figure 4.2 and 4.3,for instance).This result means that the effective conductivity value is most sensitive to the changes of ki,if the reinforcement volume ratio is maximal,which is predictable result and it positively validates this homogenisation method. The smallest sensitivity of to the parameter k can be noted for r tending to 0,while the inverse relation is observed with respect to the reinforcement volume fraction.The variability of the sensitivity surface for with respect to the heat194 Computational Mechanics of Composite Materials Figure 4.8. Material sensitivity of k(eff) in 3D problem to k1 Figure 4.9. Sensitivity of k(eff) in 3D problem to vf Analysing numerical results it can be observed that the effective heat conductivity surface has an analogous shapes for 1D, 2D and 3D composites. However the values of this coefficient obtained for the same reinforcement ratio are largest for 3D composite with spherical inclusion, next largest for 2D fibre￾reinforced composite, and smallest for the 1D case. Therefore, 3D composites seem to be most optimal - using the same volume of reinforcement, the highest value of the effective material property is obtained. According to engineering intuition, it is found that increasing both k1 and vf an increasing of final value of k (eff) is obtained. The results of sensitivity studies presented in Figures 4.3, 4.6 and 4.9 make it possible to observe the greatest sensitivity of composite effective characteristics with respect to both design parameters (k1 and vf) for extremely small values of the coefficient k1 and the largest value of the reinforcement ratio. The sensitivity gradients of k (eff) with respect to vf have almost constant value, while with respect to k1 are efficiently nonlinear and reach the maximum for vf=0.5 (cf. Figure 4.2 and 4.3, for instance). This result means that the effective conductivity value is most sensitive to the changes of k1, if the reinforcement volume ratio is maximal, which is predictable result and it positively validates this homogenisation method. The smallest sensitivity of k (eff) to the parameter k1 can be noted for vf tending to 0, while the inverse relation is observed with respect to the reinforcement volume fraction. The variability of the sensitivity surface for k(eff) with respect to the heat