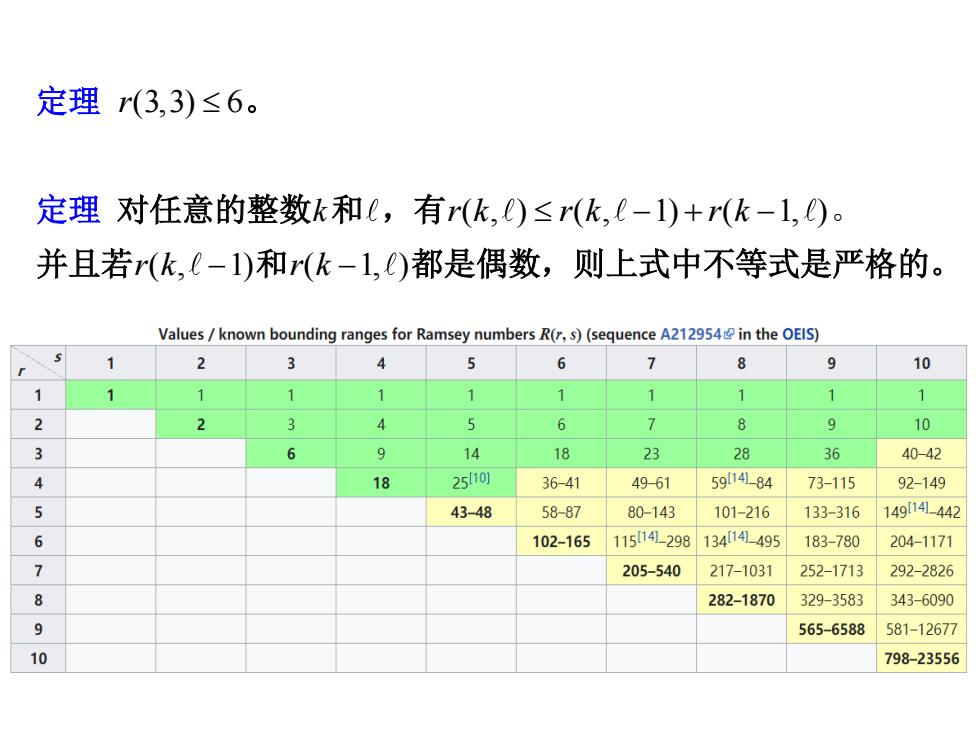
定理r(3,3)≤6。 定理对任意的整数k和L,有(k,)≤(k,(-1)+(k-1,)。 并且若r(k,(-1)和（飞-1，）都是偶数，则上式中不等式是严格的。 Values known bounding ranges for Ramsey numbers R(r,s)(sequence A212954 in the OEIS) 2 3 6 9 10 1 1 1 2 1 1 1 2 3 6 7 9 10 6 9 14 18 23 28 36 40-42 4 18 25f101 36-41 49-61 5914184 73-115 92-149 43-48 58-87 80-143 101-216 133-316 149[149-442 6 102-165 115141-298134[141-495 183-780 204-1171 205-540 217-1031 252-1713 292-2826 282-1870 329-3583 343-6090 9 565-6588 581-12677 10 798-23556 定理 r(3,3) 6  。 定理 对任意的整数k和 ，有r k r k r k ( , ) ( , 1) ( 1, )  − + − 。 并且若r k( , 1) − 和r k( 1, ) − 都是偶数，则上式中不等式是严格的