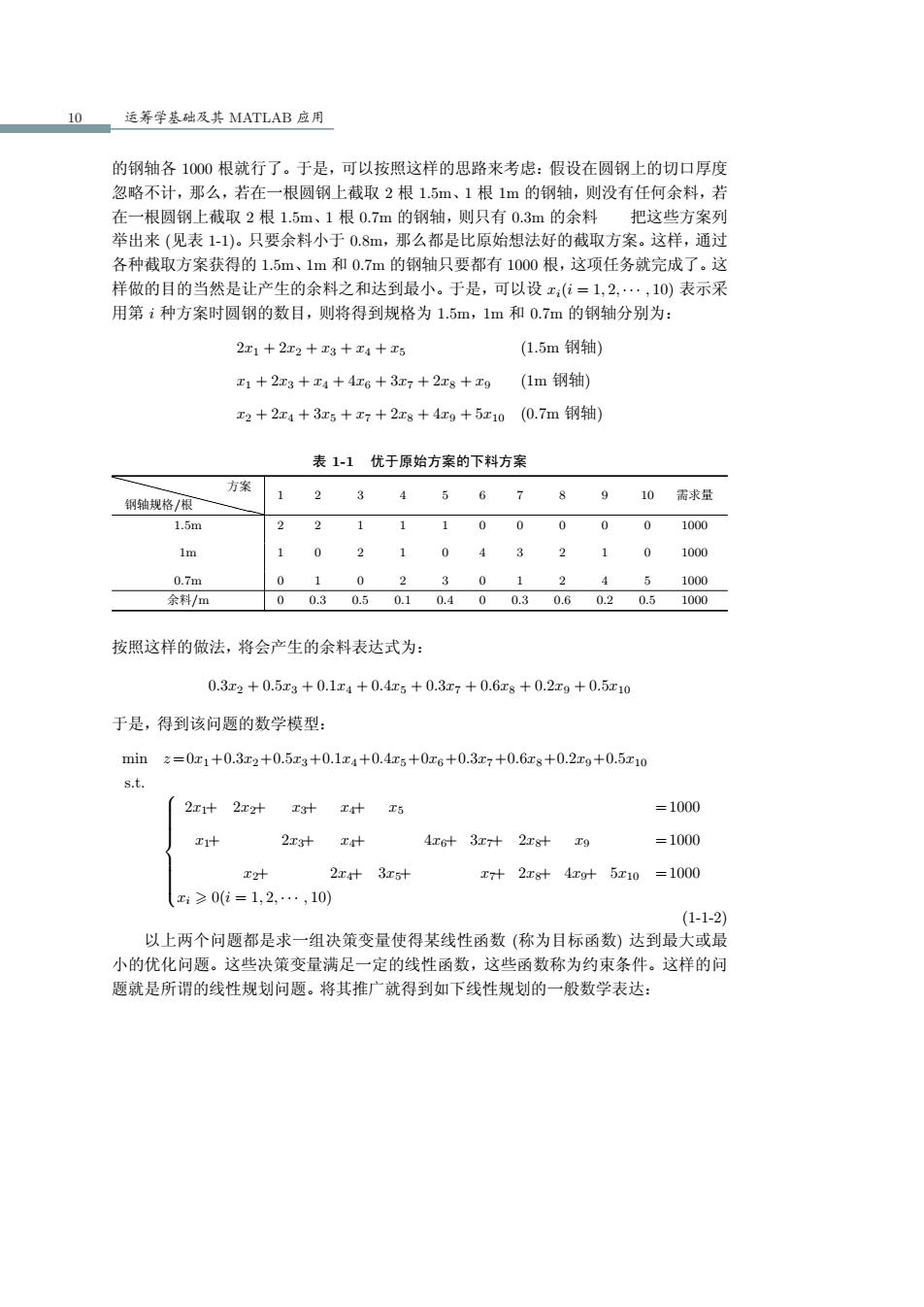
10 运筹学基础及其MATLAB应用 的钢轴各1000根就行了。于是，可以按照这样的思路来考虑：假设在圆钢上的切口厚度 忽略不计，那么，若在一根圆钢上截取2根1.5m、1根1m的钢轴，则没有任何余料，若 在一根圆钢上截取2根1.5m、1根0.7m的钢轴，则只有0.3m的余料把这些方案列 举出来（见表1-1）。只要余料小于0.8m,那么都是比原始想法好的截取方案。这样，通过 各种截取方案获得的1.5m、1m和0.7m的钢轴只要都有1000根，这项任务就完成了。这 样做的目的当然是让产生的余料之和达到最小。于是，可以设x,(亿=1,2，·，10)表示采 用第i种方案时圆钢的数目，则将得到规格为1.5m,1m和0.7m的钢轴分别为： 2x1+2x2+E3+x4+工5 (1.5m钢轴) x1+2x3+I4+4x6+3x7+2x8+xg (1m钢轴) x2+2x4+3x5+x7+2z8+4xg+5x10(0.7m钢轴) 表1-1优于原始方案的下料方案 方案 1 2 3 4 5 67 8 9 10 需求量 钢轴规格/根 1.5m 2 2 1 100000 1000 1m 0 2 1 0 43210 1000 0.7m 0 1 0 2 3 0 1 5 1000 余料/m 00.30.50.10.400.30.60.20.51000 按照这样的做法，将会产生的余料表达式为： 0.3z2+0.5x3+0.1x4+0.4r5+0.3x7+0.6z8+0.2xg+0.5z10 于是，得到该问题的数学模型： minz=0x1+0.3x2+0.5x3+0.1x4+0.4z5+0x6+0.3x7+0.6x8+0.2xg+0.5x10 s.t. 2x1+2x2+ =1000 E1十 2x3十x十 4x6+3x7+2x8+xg =1000 x2十 2z4十3x5十 x7+2x8+4xg十5x10=1000 x≥0(i=1,2,·,10) (1-1-2) 以上两个问题都是求一组决策变量使得某线性函数（称为目标函数）达到最大或最 小的优化问题。这些决策变量满足一定的线性函数，这些函数称为约束条件。这样的问 题就是所谓的线性规划问题。将其推广就得到如下线性规划的一般数学表达：10 运筹学基础及其 MATLAB 应用 的钢轴各 1000 根就行了。于是，可以按照这样的思路来考虑：假设在圆钢上的切口厚度 忽略不计，那么，若在一根圆钢上截取 2 根 1.5m、1 根 1m 的钢轴，则没有任何余料，若 在一根圆钢上截取 2 根 1.5m、1 根 0.7m 的钢轴，则只有 0.3m 的余料……把这些方案列 举出来 (见表 1-1)。只要余料小于 0.8m，那么都是比原始想法好的截取方案。这样，通过 各种截取方案获得的 1.5m、1m 和 0.7m 的钢轴只要都有 1000 根，这项任务就完成了。这 样做的目的当然是让产生的余料之和达到最小。于是，可以设 xi(i = 1, 2, · · · , 10) 表示采 用第 i 种方案时圆钢的数目，则将得到规格为 1.5m，1m 和 0.7m 的钢轴分别为： 2x1 + 2x2 + x3 + x4 + x5 (1.5m 钢轴) x1 + 2x3 + x4 + 4x6 + 3x7 + 2x8 + x9 (1m 钢轴) x2 + 2x4 + 3x5 + x7 + 2x8 + 4x9 + 5x10 (0.7m 钢轴) 表 1-1 优于原始方案的下料方案 ❳ 钢 ❳ 轴 ❳ 规 ❳ 格 ❳ /根 ❳❳❳❳❳ 方案 1 2 3 4 5 6 7 8 9 10 需求量 1.5m 2 2 1 1 1 0 0 0 0 0 1000 1m 1 0 2 1 0 4 3 2 1 0 1000 0.7m 0 1 0 2 3 0 1 2 4 5 1000 余料/m 0 0.3 0.5 0.1 0.4 0 0.3 0.6 0.2 0.5 1000 按照这样的做法，将会产生的余料表达式为： 0.3x2 + 0.5x3 + 0.1x4 + 0.4x5 + 0.3x7 + 0.6x8 + 0.2x9 + 0.5x10 于是，得到该问题的数学模型： min z= 0x1+0.3x2+0.5x3+0.1x4+0.4x5+0x6+0.3x7+0.6x8+0.2x9+0.5x10 s.t.    2x1+ 2x2+ x3+ x4+ x5 = 1000 x1+ 2x3+ x4+ 4x6+ 3x7+ 2x8+ x9 = 1000 x2+ 2x4+ 3x5+ x7+ 2x8+ 4x9+ 5x10 = 1000 xi > 0(i = 1, 2, · · · , 10) (1-1-2) 以上两个问题都是求一组决策变量使得某线性函数 (称为目标函数) 达到最大或最 小的优化问题。这些决策变量满足一定的线性函数，这些函数称为约束条件。这样的问 题就是所谓的线性规划问题。将其推广就得到如下线性规划的一般数学表达：