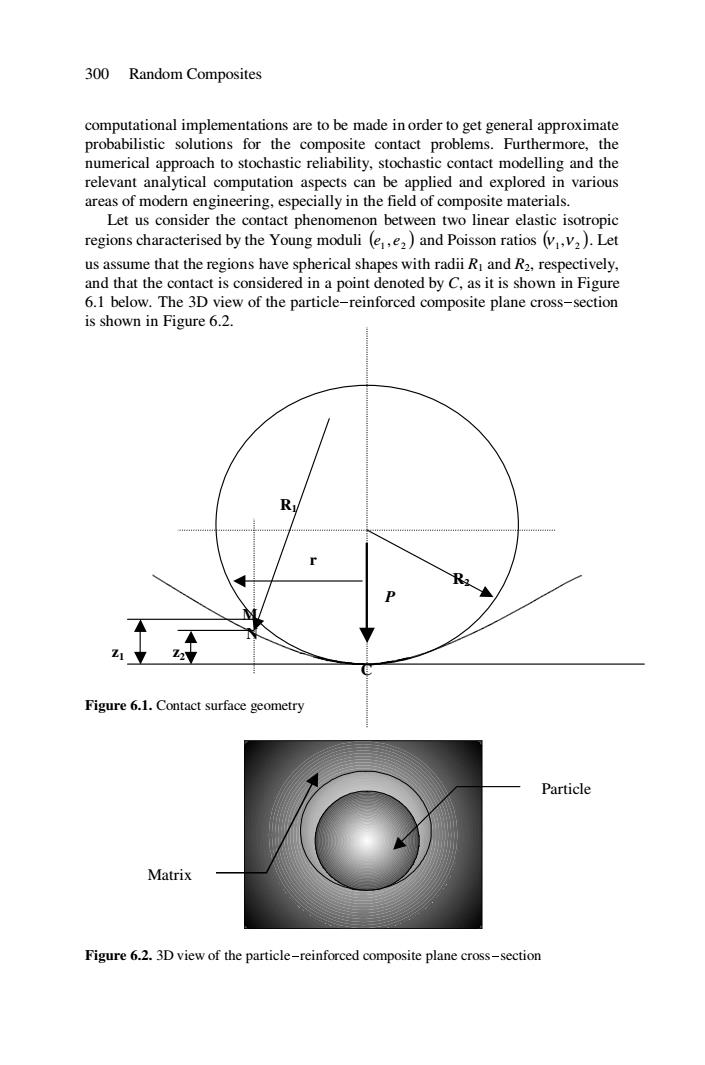
300 Random Composites computational implementations are to be made in order to get general approximate probabilistic solutions for the composite contact problems.Furthermore,the numerical approach to stochastic reliability,stochastic contact modelling and the relevant analytical computation aspects can be applied and explored in various areas of modern engineering,especially in the field of composite materials. Let us consider the contact phenomenon between two linear elastic isotropic regions characterised by the Young moduli (e,e2)and Poisson ratios (v,v2).Let us assume that the regions have spherical shapes with radii R and R2,respectively, and that the contact is considered in a point denoted by C,as it is shown in Figure 6.1 below.The 3D view of the particle-reinforced composite plane cross-section is shown in Figure 6.2. R Z17 Figure 6.1.Contact surface geometry Particle Matrix Figure 6.2.3D view of the particle-reinforced composite plane cross-section300 Random Composites computational implementations are to be made in order to get general approximate probabilistic solutions for the composite contact problems. Furthermore, the numerical approach to stochastic reliability, stochastic contact modelling and the relevant analytical computation aspects can be applied and explored in various areas of modern engineering, especially in the field of composite materials. Let us consider the contact phenomenon between two linear elastic isotropic regions characterised by the Young moduli ( ) 1 2 e , e and Poisson ratios ( ) 1 2 ν ,ν . Let us assume that the regions have spherical shapes with radii R1 and R2, respectively, and that the contact is considered in a point denoted by C, as it is shown in Figure 6.1 below. The 3D view of the particle-reinforced composite plane cross-section is shown in Figure 6.2. R1 r R2 P M N z1 z2 C Figure 6.1. Contact surface geometry Figure 6.2. 3D view of the particle-reinforced composite plane cross-section Particle Matrix