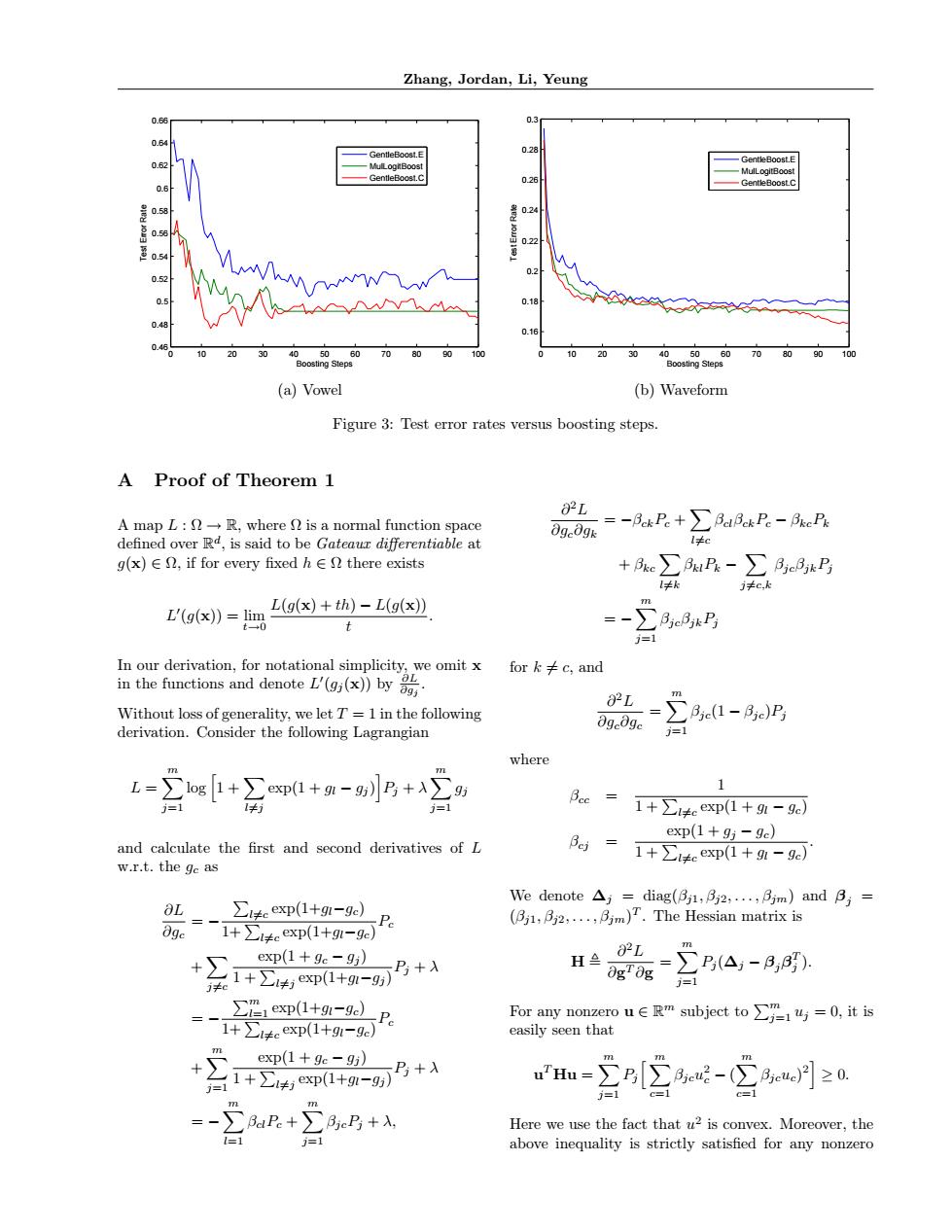
Zhang,Jordan,Li,Yeung 0.3 0.6 -GeotleBoostE 028 MulLogitBoost 一GentleBoost..E MulLogitBoost GentleBoost.C 0.26 0.2 02 30 405060708090 0 90 5060 70 90 100 Boosting Steps Boosting Steps (a)Vowel (b)Waveform Figure 3:Test error rates versus boosting steps. A Proof of Theorem 1 02L A map L:-R,where is a normal function space 0ge0gk =-ikP.+∑a8kP。-cPs defined over Rd,is said to be Gateaur differentiable at l≠c g(x)∈2，if for every fixed h∈2 there exists +e∑3uP-∑3c3kB I≠k j≠c,k L'(g(x))=lim L(g(x)+th)-L(g(x)) t+0 j=1 In our derivation,for notational simplicity,we omit x fork≠c,and in the functions and denote L'(g())by 8 02L m Without loss of generality,we let T=1 in the following Be(1-月c) derivation.Consider the following Lagrangian OgeOge j=1 where -2sf++m-B+ m 1 j=1 1+∑4eexp(1+9-9e】 Bej exp(1+95-9c） and calculate the first and second derivatives of L w.r.t.the ge as 1+∑i4eexp(1+91-9c) 0L_∑i4eexp(1+9-9e） We denote△，=diag(3i1,fi2,.,月m)and B;= 两.i+4ep(1+9u-gB (2....Bm)T.The Hessian matrix is m exp(1+9c-95) 82L +工1+∑p1+m=B+入 H -∑P(A-3,) ∂g0g j=1 ∑"exp(1+-9P =-1+4.exp(1+91-9e】 For any nonzero u∈msubject to∑l4=0,itis easily seen that exp(1+gc-9i】 ++9-B+小 uHm-∑p[呢-（月≥0 j=1 一%R+三.+ m m Here we use the fact that u2 is convex.Moreover,the =1 above inequality is strictly satisfied for any nonzeroZhang, Jordan, Li, Yeung 0 10 20 30 40 50 60 70 80 90 100 0.46 0.48 0.5 0.52 0.54 0.56 0.58 0.6 0.62 0.64 0.66 Boosting Steps Test Error Rate GentleBoost.E MulLogitBoost GentleBoost.C 0 10 20 30 40 50 60 70 80 90 100 0.16 0.18 0.2 0.22 0.24 0.26 0.28 0.3 Boosting Steps Test Error Rate GentleBoost.E MulLogitBoost GentleBoost.C (a) Vowel (b) Waveform Figure 3: Test error rates versus boosting steps. A Proof of Theorem 1 A map L : Ω → R, where Ω is a normal function space defined over R d , is said to be Gateaux differentiable at g(x) ∈ Ω, if for every fixed h ∈ Ω there exists L ′ (g(x)) = limt→0 L(g(x) + th) − L(g(x)) t . In our derivation, for notational simplicity, we omit x in the functions and denote L ′ (gj (x)) by ∂L ∂gj . Without loss of generality, we let T = 1 in the following derivation. Consider the following Lagrangian L = Xm j=1 log h 1 +X l6=j exp(1 + gl − gj ) i Pj + λ Xm j=1 gj and calculate the first and second derivatives of L w.r.t. the gc as ∂L ∂gc = − P l6=c exp(1+gl−gc) 1+P l6=c exp(1+gl−gc) Pc + X j6=c exp(1 + gc − gj ) 1 + P l6=j exp(1+gl−gj ) Pj + λ = − Pm l=1 exp(1+gl−gc) 1+P l6=c exp(1+gl−gc) Pc + Xm j=1 exp(1 + gc − gj ) 1 + P l6=j exp(1+gl−gj ) Pj + λ = − Xm l=1 βclPc + Xm j=1 βjcPj + λ, ∂ 2L ∂gc∂gk = −βckPc + X l6=c βclβckPc − βkcPk + βkcX l6=k βklPk − X j6=c,k βjcβjkPj = − Xm j=1 βjcβjkPj for k 6= c, and ∂ 2L ∂gc∂gc = Xm j=1 βjc(1 − βjc)Pj where βcc = 1 1 + P l6=c exp(1 + gl − gc) βcj = exp(1 + gj − gc) 1 + P l6=c exp(1 + gl − gc) . We denote ∆j = diag(βj1, βj2, . . . , βjm) and βj = (βj1, βj2, . . . , βjm) T . The Hessian matrix is H , ∂ 2L ∂g T ∂g = Xm j=1 Pj (∆j − βjβ T j ). For any nonzero u ∈ R m subject to Pm j=1 uj = 0, it is easily seen that u T Hu = Xm j=1 Pj hXm c=1 βjcu 2 c − ( Xm c=1 βjcuc) 2 i ≥ 0. Here we use the fact that u 2 is convex. Moreover, the above inequality is strictly satisfied for any nonzero