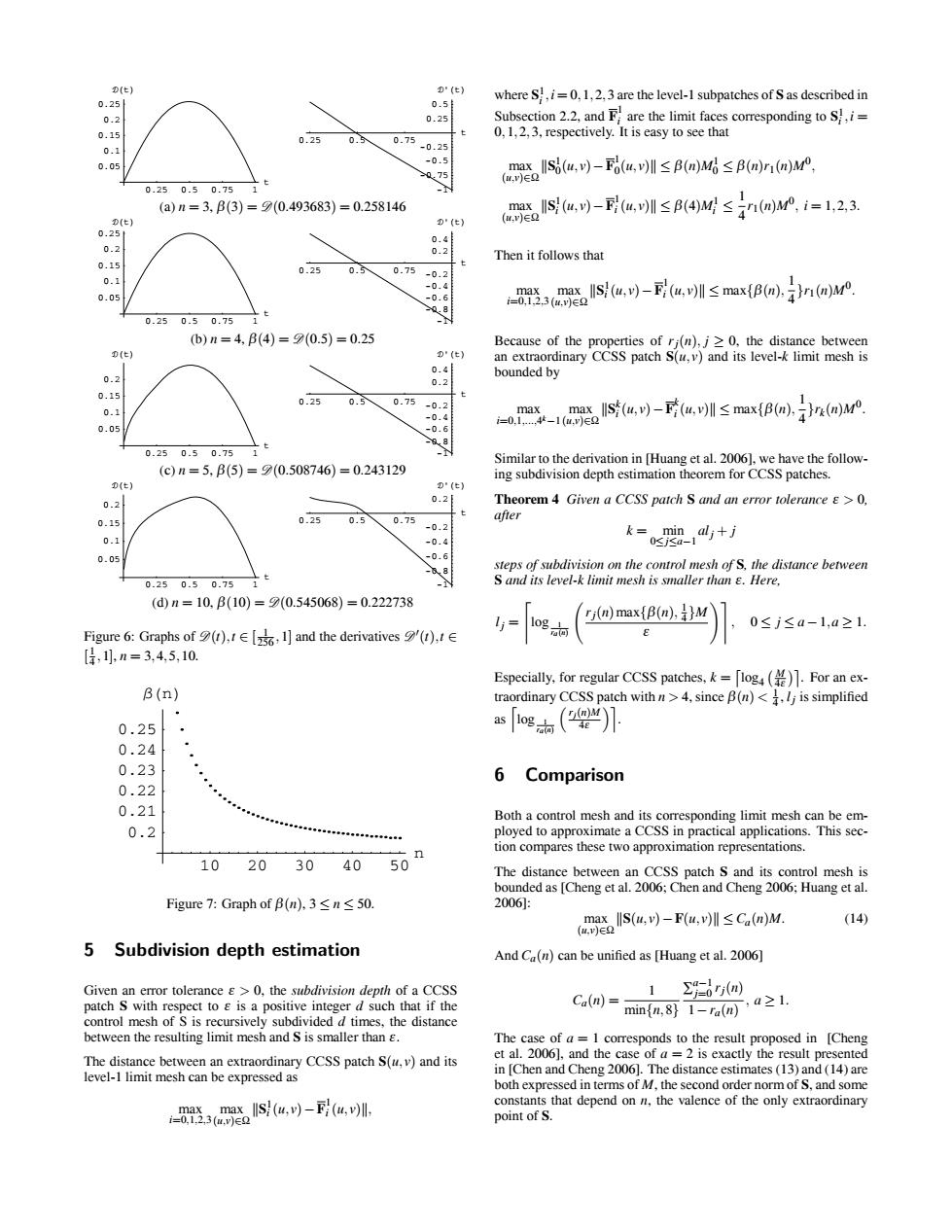
2"高oam ( 二A04n6-2 母W-a,1≤4Msn(mwe1e1,23 Then it follows that n/盆 (-Fv m(B)im . 0508740=0.24312 + da-1mA10-545-2273 在920e女ine9e =s(（me）l.0sea-l2 B (n 6 Comparison 10203040504 he d Figure7:Gnph of(a以3≤n≤50 14 5 Subdivision depth estimation c-m两器得210.25 0.5 0.75 1 t 0.05 0.1 0.15 0.2 0.25 t 0.25 0.5 0.75 t 1 0.75 0.5 0.25 0.25 0.5 't (a) n = 3, β(3) = D(0.493683) = 0.258146 0.25 0.5 0.75 1 t 0.05 0.1 0.15 0.2 0.25 t 0.25 0.5 0.75 t 1 0.8 0.6 0.4 0.2 0.2 0.4 't (b) n = 4, β(4) = D(0.5) = 0.25 0.25 0.5 0.75 1 t 0.05 0.1 0.15 0.2 t 0.25 0.5 0.75 t 1 0.8 0.6 0.4 0.2 0.2 0.4 't (c) n = 5, β(5) = D(0.508746) = 0.243129 0.25 0.5 0.75 1 t 0.05 0.1 0.15 0.2 t 0.25 0.5 0.75 t 1 0.8 0.6 0.4 0.2 0.2 't (d) n = 10, β(10) = D(0.545068) = 0.222738 Figure 6: Graphs of D(t),t ∈ [ 1 256 ,1] and the derivatives D (t),t ∈ [ 1 4 ,1], n = 3,4,5,10. 10 20 30 40 50 n 0.2 0.21 0.22 0.23 0.24 0.25 Βn Figure 7: Graph of β(n), 3 ≤ n ≤ 50. 5 Subdivision depth estimation Given an error tolerance ε > 0, the subdivision depth of a CCSS patch S with respect to ε is a positive integer d such that if the control mesh of S is recursively subdivided d times, the distance between the resulting limit mesh and S is smaller than ε. The distance between an extraordinary CCSS patch S(u, v) and its level-1 limit mesh can be expressed as max i=0,1,2,3 max (u,v)∈Ω S1 i (u, v)−F1 i (u, v), where S1 i ,i = 0,1,2,3 are the level-1 subpatches of S as described in Subsection 2.2, and F1 i are the limit faces corresponding to S1 i ,i = 0,1,2,3, respectively. It is easy to see that max (u,v)∈Ω S1 0(u, v)−F1 0(u, v) ≤ β(n)M1 0 ≤ β(n)r1(n)M0, max (u,v)∈Ω S1 i (u, v)−F1 i (u, v) ≤ β(4)M1 i ≤ 1 4 r1(n)M0, i = 1,2,3. Then it follows that max i=0,1,2,3 max (u,v)∈Ω S1 i (u, v)−F1 i (u, v) ≤ max{β(n), 1 4 }r1(n)M0. Because of the properties of rj(n), j ≥ 0, the distance between an extraordinary CCSS patch S(u, v) and its level-k limit mesh is bounded by max i=0,1,...,4k−1 max (u,v)∈Ω Sk i (u, v)−Fk i (u, v) ≤ max{β(n), 1 4 }rk(n)M0. Similar to the derivation in [Huang et al. 2006], we have the follow￾ing subdivision depth estimation theorem for CCSS patches. Theorem 4 Given a CCSS patch S and an error tolerance ε > 0, after k = min 0≤j≤a−1 alj + j steps of subdivision on the control mesh of S, the distance between S and its level-k limit mesh is smaller than ε. Here, lj =  log 1 ra(n)  rj(n)max{β(n), 1 4 }M ε , 0 ≤ j ≤ a−1,a ≥ 1. Especially, for regular CCSS patches, k =  log4  M 4ε . For an ex￾traordinary CCSS patch with n > 4, since β(n) < 1 4 , lj is simplified as  log 1 ra(n) rj(n)M 4ε . 6 Comparison Both a control mesh and its corresponding limit mesh can be em￾ployed to approximate a CCSS in practical applications. This sec￾tion compares these two approximation representations. The distance between an CCSS patch S and its control mesh is bounded as [Cheng et al. 2006; Chen and Cheng 2006; Huang et al. 2006]: max (u,v)∈Ω S(u, v)−F(u, v) ≤ Ca(n)M. (14) And Ca(n) can be unified as [Huang et al. 2006] Ca(n) = 1 min{n,8} ∑a−1 j=0 rj(n) 1−ra(n) , a ≥ 1. The case of a = 1 corresponds to the result proposed in [Cheng et al. 2006], and the case of a = 2 is exactly the result presented in [Chen and Cheng 2006]. The distance estimates (13) and (14) are both expressed in terms of M, the second order norm of S, and some constants that depend on n, the valence of the only extraordinary point of S.