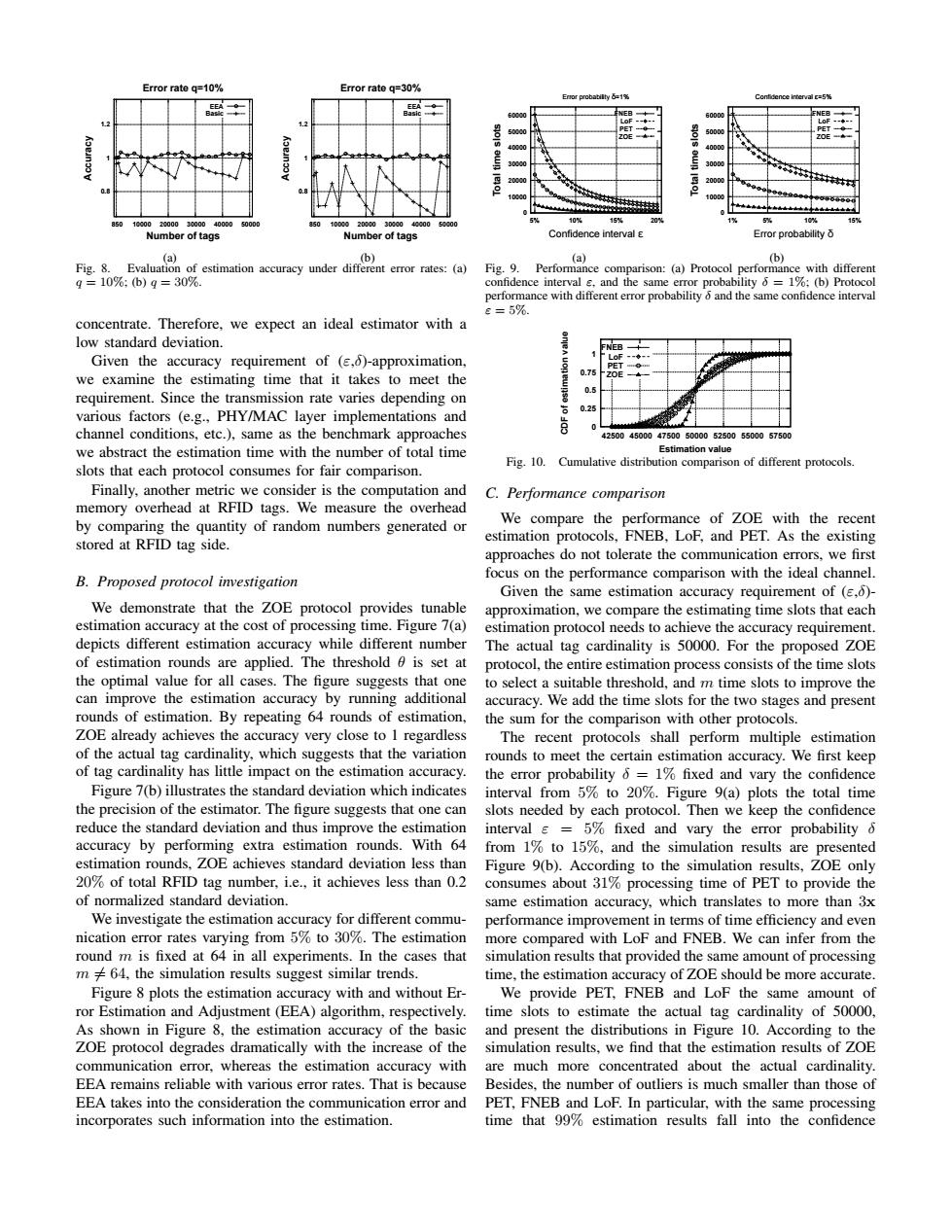
Error rate q=10% Error rate q=30% Eror probabilty 6=1% NEB 5001 4000 3000 2000 t000 10% 15% 20 10% 15 50 2000030000 40000 5000 200 30c Number of tags Number of tags Confidence interval E Error probability a (b) a (b) Fig.8.Evaluation of estimation accuracy under different error rates:(a) Fig.9.Performance comparison:(a)Protocol performance with different 9=10%:b)9=30% confidence interval s,and the same error probability =1%:(b)Protocol performance with different error probability 6 and the same confidence interval =5%. concentrate.Therefore,we expect an ideal estimator with a low standard deviation. Given the accuracy requirement of (,6)-approximation, we examine the estimating time that it takes to meet the 0.75 0.5 requirement.Since the transmission rate varies depending on various factors (e.g.,PHY/MAC layer implementations and 0.25 0 channel conditions,etc.),same as the benchmark approaches 42500450004750050000525005500057500 we abstract the estimation time with the number of total time Estimation value Fig.10. Cumulative distribution comparison of different protocols. slots that each protocol consumes for fair comparison. Finally,another metric we consider is the computation and C.Performance comparison memory overhead at RFID tags.We measure the overhead by comparing the quantity of random numbers generated or We compare the performance of ZOE with the recent stored at RFID tag side. estimation protocols,FNEB,LoF,and PET.As the existing approaches do not tolerate the communication errors,we first B.Proposed protocol investigation focus on the performance comparison with the ideal channel. Given the same estimation accuracy requirement of (e,6)- We demonstrate that the ZOE protocol provides tunable approximation,we compare the estimating time slots that each estimation accuracy at the cost of processing time.Figure 7(a) estimation protocol needs to achieve the accuracy requirement depicts different estimation accuracy while different number The actual tag cardinality is 50000.For the proposed ZOE of estimation rounds are applied.The threshold is set at protocol,the entire estimation process consists of the time slots the optimal value for all cases.The figure suggests that one to select a suitable threshold,and m time slots to improve the can improve the estimation accuracy by running additional accuracy.We add the time slots for the two stages and present rounds of estimation.By repeating 64 rounds of estimation, the sum for the comparison with other protocols. ZOE already achieves the accuracy very close to 1 regardless The recent protocols shall perform multiple estimation of the actual tag cardinality,which suggests that the variation rounds to meet the certain estimation accuracy.We first keep of tag cardinality has little impact on the estimation accuracy. the error probability 6=1%fixed and vary the confidence Figure 7(b)illustrates the standard deviation which indicates interval from 5%to 20%.Figure 9(a)plots the total time the precision of the estimator.The figure suggests that one can slots needed by each protocol.Then we keep the confidence reduce the standard deviation and thus improve the estimation interval s=5%fixed and vary the error probability 6 accuracy by performing extra estimation rounds.With 64 from 1%to 15%,and the simulation results are presented estimation rounds.ZOE achieves standard deviation less than Figure 9(b).According to the simulation results,ZOE only 20%of total RFID tag number,i.e..it achieves less than 0.2 consumes about 31%processing time of PET to provide the of normalized standard deviation. same estimation accuracy,which translates to more than 3x We investigate the estimation accuracy for different commu- performance improvement in terms of time efficiency and even nication error rates varying from 5%to 30%.The estimation more compared with LoF and FNEB.We can infer from the round m is fixed at 64 in all experiments.In the cases that simulation results that provided the same amount of processing m 64,the simulation results suggest similar trends. time,the estimation accuracy of ZOE should be more accurate. Figure 8 plots the estimation accuracy with and without Er- We provide PET,FNEB and LoF the same amount of ror Estimation and Adjustment(EEA)algorithm,respectively. time slots to estimate the actual tag cardinality of 50000, As shown in Figure 8,the estimation accuracy of the basic and present the distributions in Figure 10.According to the ZOE protocol degrades dramatically with the increase of the simulation results,we find that the estimation results of ZOE communication error,whereas the estimation accuracy with are much more concentrated about the actual cardinality. EEA remains reliable with various error rates.That is because Besides.the number of outliers is much smaller than those of EEA takes into the consideration the communication error and PET,FNEB and LoF.In particular,with the same processing incorporates such information into the estimation. time that 99%estimation results fall into the confidence0.8 1 1.2 850 10000 20000 30000 40000 50000 Accuracy Number of tags Error rate q=10% EEA Basic (a) 0.8 1 1.2 850 10000 20000 30000 40000 50000 Accuracy Number of tags Error rate q=30% EEA Basic (b) Fig. 8. Evaluation of estimation accuracy under different error rates: (a) q = 10%; (b) q = 30%. concentrate. Therefore, we expect an ideal estimator with a low standard deviation. Given the accuracy requirement of (ε,δ)-approximation, we examine the estimating time that it takes to meet the requirement. Since the transmission rate varies depending on various factors (e.g., PHY/MAC layer implementations and channel conditions, etc.), same as the benchmark approaches we abstract the estimation time with the number of total time slots that each protocol consumes for fair comparison. Finally, another metric we consider is the computation and memory overhead at RFID tags. We measure the overhead by comparing the quantity of random numbers generated or stored at RFID tag side. B. Proposed protocol investigation We demonstrate that the ZOE protocol provides tunable estimation accuracy at the cost of processing time. Figure 7(a) depicts different estimation accuracy while different number of estimation rounds are applied. The threshold θ is set at the optimal value for all cases. The figure suggests that one can improve the estimation accuracy by running additional rounds of estimation. By repeating 64 rounds of estimation, ZOE already achieves the accuracy very close to 1 regardless of the actual tag cardinality, which suggests that the variation of tag cardinality has little impact on the estimation accuracy. Figure 7(b) illustrates the standard deviation which indicates the precision of the estimator. The figure suggests that one can reduce the standard deviation and thus improve the estimation accuracy by performing extra estimation rounds. With 64 estimation rounds, ZOE achieves standard deviation less than 20% of total RFID tag number, i.e., it achieves less than 0.2 of normalized standard deviation. We investigate the estimation accuracy for different commu￾nication error rates varying from 5% to 30%. The estimation round m is fixed at 64 in all experiments. In the cases that m 6= 64, the simulation results suggest similar trends. Figure 8 plots the estimation accuracy with and without Er￾ror Estimation and Adjustment (EEA) algorithm, respectively. As shown in Figure 8, the estimation accuracy of the basic ZOE protocol degrades dramatically with the increase of the communication error, whereas the estimation accuracy with EEA remains reliable with various error rates. That is because EEA takes into the consideration the communication error and incorporates such information into the estimation. 0 10000 20000 30000 40000 50000 60000 5% 10% 15% 20% Total time slots Confidence interval ε Error probability δ=1% FNEB LoF PET ZOE (a) 0 10000 20000 30000 40000 50000 60000 1% 5% 10% 15% Total time slots Error probability δ Confidence interval ε=5% FNEB LoF PET ZOE (b) Fig. 9. Performance comparison: (a) Protocol performance with different confidence interval ε, and the same error probability δ = 1%; (b) Protocol performance with different error probability δ and the same confidence interval ε = 5%. 0 0.25 0.5 0.75 1 42500 45000 47500 50000 52500 55000 57500 CDF of estimation value Estimation value FNEB LoF PET ZOE Fig. 10. Cumulative distribution comparison of different protocols. C. Performance comparison We compare the performance of ZOE with the recent estimation protocols, FNEB, LoF, and PET. As the existing approaches do not tolerate the communication errors, we first focus on the performance comparison with the ideal channel. Given the same estimation accuracy requirement of (ε,δ)- approximation, we compare the estimating time slots that each estimation protocol needs to achieve the accuracy requirement. The actual tag cardinality is 50000. For the proposed ZOE protocol, the entire estimation process consists of the time slots to select a suitable threshold, and m time slots to improve the accuracy. We add the time slots for the two stages and present the sum for the comparison with other protocols. The recent protocols shall perform multiple estimation rounds to meet the certain estimation accuracy. We first keep the error probability δ = 1% fixed and vary the confidence interval from 5% to 20%. Figure 9(a) plots the total time slots needed by each protocol. Then we keep the confidence interval ε = 5% fixed and vary the error probability δ from 1% to 15%, and the simulation results are presented Figure 9(b). According to the simulation results, ZOE only consumes about 31% processing time of PET to provide the same estimation accuracy, which translates to more than 3x performance improvement in terms of time efficiency and even more compared with LoF and FNEB. We can infer from the simulation results that provided the same amount of processing time, the estimation accuracy of ZOE should be more accurate. We provide PET, FNEB and LoF the same amount of time slots to estimate the actual tag cardinality of 50000, and present the distributions in Figure 10. According to the simulation results, we find that the estimation results of ZOE are much more concentrated about the actual cardinality. Besides, the number of outliers is much smaller than those of PET, FNEB and LoF. In particular, with the same processing time that 99% estimation results fall into the confidence