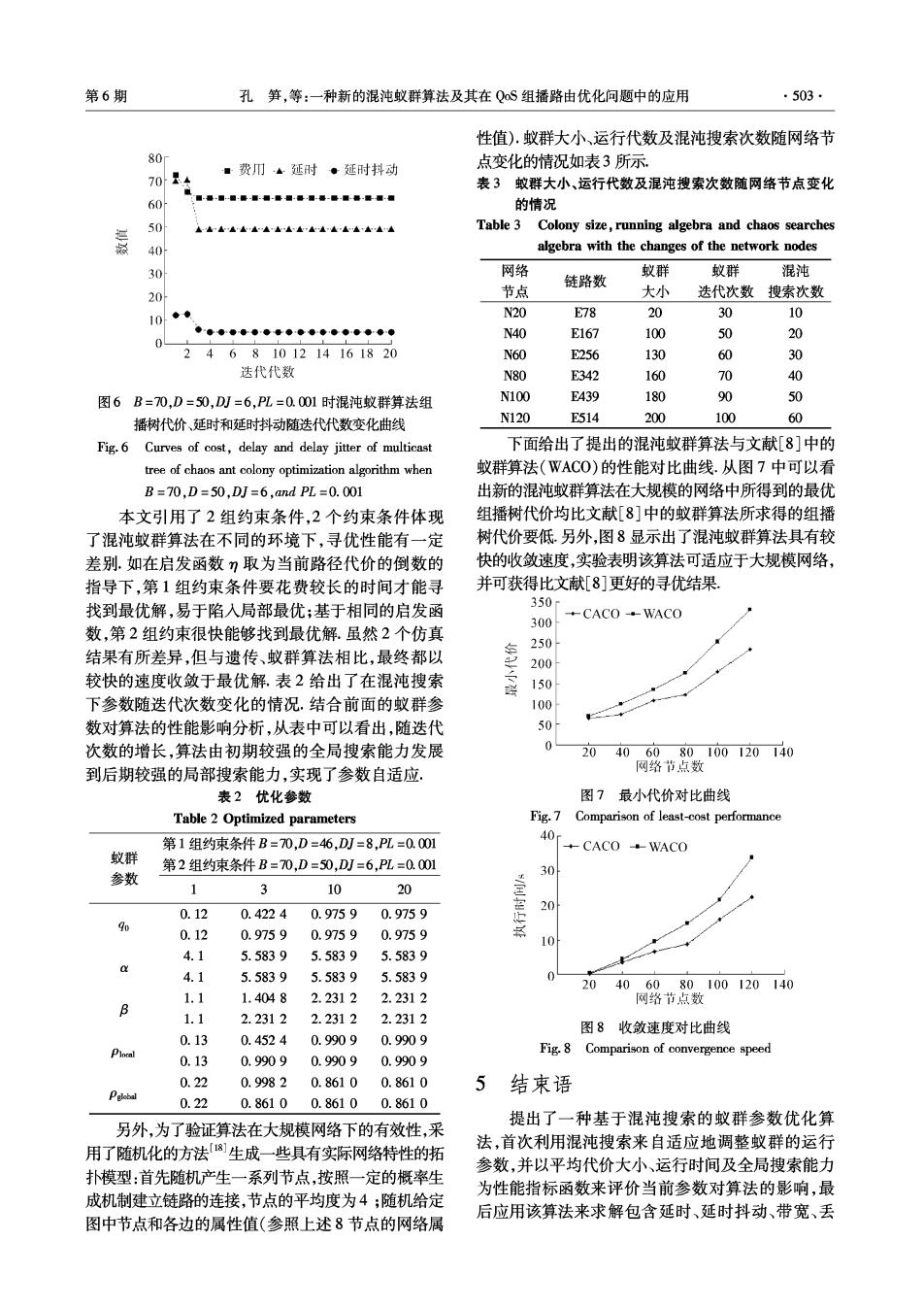
第6期 孔笋，等：一种新的混沌蚁群算法及其在QS组播路由优化向题中的应用 ·503· 性值)，蚁群大小、运行代数及混沌搜索次数随网络节 80 点变化的情况如表3所示. 701+ ■费川。延时·延时抖动 表3蚊群大小、运行代数及混沌搜索次数随网络节点变化 60 ■得-■国警■指-层国-量国暑-器■琴-层国■ 的情况 延 50 ▲hh▲山▲A~h▲~A▲▲h▲▲ Table 3 Colony size,running algebra and chaos searches 40 algebra with the changes of the network nodes 30 网络 蚁群 蚁群 混沌 链路数 20 节点 大小 迭代次数搜索次数 10◆◆ N20 E78 20 30 10 ●◆●◆●●t◆◆◆g◆9●。● N40 E167 100 50 20 0 2468101214161820 N60 E256 130 60 30 迭代代数 N80 E342 160 70 40 图6B=70,D=50,DJ=6,PL=0.001时混沌蚁群算法组 N100 E439 180 90 50 播树代价、延时和延时抖动随迭代代数变化曲线 N120 E514 200 100 60 Fig.6 Curves of cost,delay and delay jitter of multicast 下面给出了提出的混沌蚁群算法与文献[8]中的 tree of chaos ant colony optimization algorithm when 蚁群算法(WACO0)的性能对比曲线.从图7中可以看 B=70,D=50,DJ=6,and PL=0.001 出新的混沌蚁群算法在大规模的网络中所得到的最优 本文引用了2组约束条件，2个约束条件体现 组播树代价均比文献[8]中的蚁群算法所求得的组播 了混沌蚁群算法在不同的环境下，寻优性能有一定 树代价要低.另外，图8显示出了混沌蚁群算法具有较 差别.如在启发函数η取为当前路径代价的倒数的 快的收敛速度，实验表明该算法可适应于大规模网络， 指导下，第1组约束条件要花费较长的时间才能寻 并可获得比文献[8]更好的寻优结果 找到最优解，易于陷入局部最优；基于相同的启发函 350 CACO-WACO 300 数，第2组约束很快能够找到最优解.虽然2个仿真 250 结果有所差异，但与遗传、蚁群算法相比，最终都以 200 较快的速度收敛于最优解.表2给出了在混沌搜索 150 下参数随迭代次数变化的情况.结合前面的蚁群参 100 数对算法的性能影响分析，从表中可以看出，随迭代 50 次数的增长，算法由初期较强的全局搜索能力发展 0 20406080100120140 到后期较强的局部搜索能力，实现了参数自适应. 网路节点数 表2优化参数 图7最小代价对比曲线 Table 2 Optimized parameters Fig.7 Comparison of least-cost performance 第1组约束条件B=70,D=46,DJ=8,PL=0.001 40 CACO -WACO 蚁群 第2组约束条件B=70,D=50,DJ=6,PL=0.001 参数 30 10 20 0.12 0.4224 0.9759 0.9759 9o 0.12 0.9759 0.9759 0.9759 10 4.1 5.5839 5.5839 5.5839 4.1 5.5839 5.5839 5.5839 20 406080100120140 1.1 1.4048 2.2312 2.2312 网络节点数 B 1.1 2.2312 2.2312 2.2312 图8收敛速度对比曲线 0.13 0.4524 0.9909 0.9909 Plocal Fig.8 Comparison of convergence speed 0.13 0.9909 0.9909 0.9909 0.22 0.9982 0.8610 0.8610 结束语 Pglebal 0.22 0.86100.86100.8610 提出了一种基于混沌搜索的蚁群参数优化算 另外，为了验证算法在大规模网络下的有效性，采 用了随机化的方法8]生成一些具有实际网络特性的拓 法，首次利用混沌搜索来自适应地调整蚁群的运行 参数，并以平均代价大小、运行时间及全局搜索能力 扑模型：首先随机产生一系列节点，按照一定的概率生 为性能指标函数来评价当前参数对算法的影响，最 成机制建立链路的连接，节点的平均度为4；随机给定 后应用该算法来求解包含延时、延时抖动、带宽、丢 图中节点和各边的属性值（参照上述8节点的网络属