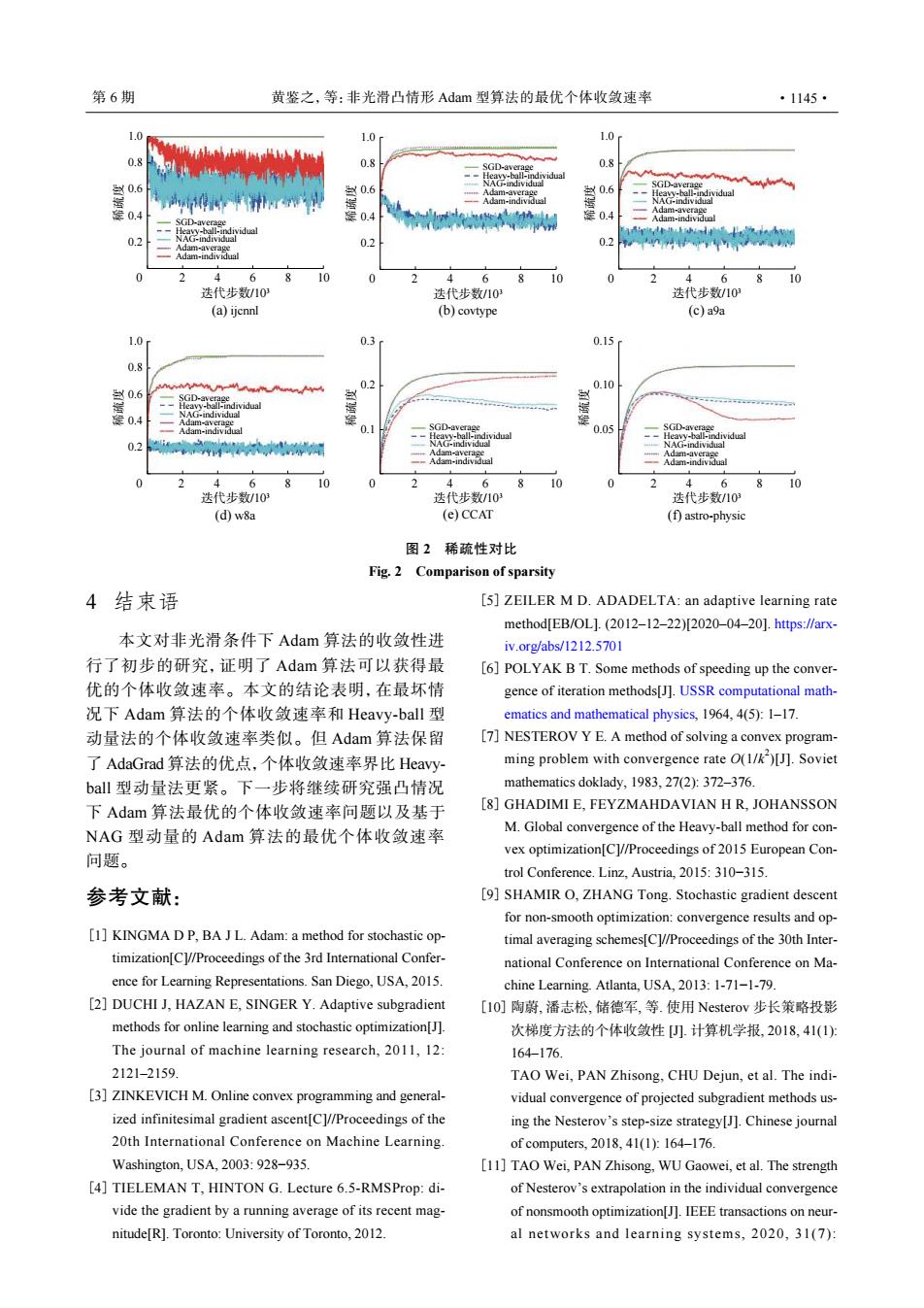
第6期 黄鉴之，等：非光滑凸情形Adam型算法的最优个体收敛速率 ·1145· 1.0 1.0 1.0 0.8 0.8 0.8 0.6 当0.6 A出Aa 0.6 SGD-aver 0.4 0.4 0.4 -Adam-individual iriv 0.2 0.2 0.2 Adam-individual nw 4 6 8 10 0 4 8 2 4 6810 迭代步数/103 迭代步数/10 选代步数/10 (a)ijcnnl (b)covtype (c)a9a 1.0 0.3 0.15r 0.8 0.10 0.6 0.4 NAG-irdividua Adam-individual 0.1 SGD-averein 0.05 0.2 d 6 8 10 0 2 4 6 8 10 0 2 4 6 8 10 迭代步数/10 迭代步数/103 迭代步数/10 (d)w8a (e)CCAT (f)astro-physic 图2稀疏性对比 Fig.2 Comparison of sparsity 4结束语 [5]ZEILER M D.ADADELTA:an adaptive learning rate method EB/0L].(2012-12-22)[2020-04-201.https:/∥arx 本文对非光滑条件下Adam算法的收敛性进 iv.org/abs/1212.5701 行了初步的研究，证明了Adam算法可以获得最 [6]POLYAK B T.Some methods of speeding up the conver- 优的个体收敛速率。本文的结论表明，在最坏情 gence of iteration methods[J].USSR computational math- 况下Adam算法的个体收敛速率和Heavy-ball型 ematics and mathematical physics,1964,4(5):1-17 动量法的个体收敛速率类似。但Adam算法保留 [7]NESTEROV Y E.A method of solving a convex program- 了AdaGrad算法的优，点，个体收敛速率界比Heavy- ming problem with convergence rate O(1/)[J].Soviet bal型动量法更紧。下一步将继续研究强凸情况 mathematics doklady,1983,27(2):372-376. 下Adam算法最优的个体收敛速率问题以及基于 [8]GHADIMI E,FEYZMAHDAVIAN H R,JOHANSSON NAG型动量的Adam算法的最优个体收敛速率 M.Global convergence of the Heavy-ball method for con- vex optimization[C]//Proceedings of 2015 European Con- 问题。 trol Conference.Linz.Austria.2015:310-315. 参考文献： [9]SHAMIR O,ZHANG Tong.Stochastic gradient descent for non-smooth optimization:convergence results and op- [1]KINGMA D P,BA J L.Adam:a method for stochastic op- timal averaging schemes[C]//Proceedings of the 30th Inter- timization[C]//Proceedings of the 3rd International Confer- national Conference on International Conference on Ma- ence for Learning Representations.San Diego,USA,2015. chine Learning.Atlanta,USA,2013:1-71-1-79. [2]DUCHI J.HAZAN E.SINGER Y.Adaptive subgradient [IO]陶蔚，潘志松，储德军，等.使用Nesterov步长策略投影 methods for online learning and stochastic optimization[J]. 次梯度方法的个体收敛性).计算机学报，2018,41(1)： The journal of machine learning research,2011,12: 164176. 2121-2159 TAO Wei,PAN Zhisong,CHU Dejun,et al.The indi- [3]ZINKEVICH M.Online convex programming and general- vidual convergence of projected subgradient methods us- ized infinitesimal gradient ascent[C]//Proceedings of the ing the Nesterov's step-size strategy[J].Chinese journal 20th International Conference on Machine Learning. of computers,2018,41(1)y164-176. Washington.USA.2003:928-935 [11]TAO Wei,PAN Zhisong,WU Gaowei,et al.The strength [4]TIELEMAN T,HINTON G.Lecture 6.5-RMSProp:di- of Nesterov's extrapolation in the individual convergence vide the gradient by a running average of its recent mag- of nonsmooth optimization[J].IEEE transactions on neur- nitude[R].Toronto:University of Toronto,2012. al networks and learning systems,2020,31(7):SGD-average Heavy-ball-individual NAG-individual Adam-average Adam-individual 1.0 0.6 0.8 0.2 0.4 0 2 4 6 8 10 (a) ijcnnl 迭代步数/103 稀疏度 SGD-average Heavy-ball-individual NAG-individual Adam-average Adam-individual 1.0 0.6 0.8 0.2 0.4 0 2 4 6 8 10 (d) w8a 迭代步数/103 稀疏度 SGD-average Heavy-ball-individual NAG-individual Adam-average Adam-individual 0.3 0.2 0.1 0 2 4 6 8 10 (e) CCAT 迭代步数/103 稀疏度 SGD-average Heavy-ball-individual NAG-individual Adam-average Adam-individual 0.15 0.10 0.05 0 2 4 6 8 10 (f) astro-physic 迭代步数/103 稀疏度 SGD-average Heavy-ball-individual NAG-individual Adam-average Adam-individual 1.0 0.6 0.8 0.2 0.4 0 2 4 6 8 10 迭代步数/103 稀疏度 (b) covtype SGD-average Heavy-ball-individual NAG-individual Adam-average Adam-individual 1.0 0.6 0.8 0.2 0.4 0 2 4 6 8 10 迭代步数/103 稀疏度 (c) a9a 图 2 稀疏性对比 Fig. 2 Comparison of sparsity 4 结束语 本文对非光滑条件下 Adam 算法的收敛性进 行了初步的研究，证明了 Adam 算法可以获得最 优的个体收敛速率。本文的结论表明，在最坏情 况下 Adam 算法的个体收敛速率和 Heavy-ball 型 动量法的个体收敛速率类似。但 Adam 算法保留 了 AdaGrad 算法的优点，个体收敛速率界比 Heavy￾ball 型动量法更紧。下一步将继续研究强凸情况 下 Adam 算法最优的个体收敛速率问题以及基于 NAG 型动量的 Adam 算法的最优个体收敛速率 问题。 参考文献： KINGMA D P, BA J L. Adam: a method for stochastic op￾timization[C]//Proceedings of the 3rd International Confer￾ence for Learning Representations. San Diego, USA, 2015. [1] DUCHI J, HAZAN E, SINGER Y. Adaptive subgradient methods for online learning and stochastic optimization[J]. The journal of machine learning research, 2011, 12: 2121–2159. [2] ZINKEVICH M. Online convex programming and general￾ized infinitesimal gradient ascent[C]//Proceedings of the 20th International Conference on Machine Learning. Washington, USA, 2003: 928−935. [3] TIELEMAN T, HINTON G. Lecture 6.5-RMSProp: di￾vide the gradient by a running average of its recent mag￾nitude[R]. Toronto: University of Toronto, 2012. [4] ZEILER M D. ADADELTA: an adaptive learning rate method[EB/OL]. (2012–12–22)[2020–04–20]. https://arx￾iv.org/abs/1212.5701 [5] POLYAK B T. Some methods of speeding up the conver￾gence of iteration methods[J]. USSR computational math￾ematics and mathematical physics, 1964, 4(5): 1–17. [6] NESTEROV Y E. A method of solving a convex program￾ming problem with convergence rate O(1/k 2 )[J]. Soviet mathematics doklady, 1983, 27(2): 372–376. [7] GHADIMI E, FEYZMAHDAVIAN H R, JOHANSSON M. Global convergence of the Heavy-ball method for con￾vex optimization[C]//Proceedings of 2015 European Con￾trol Conference. Linz, Austria, 2015: 310−315. [8] SHAMIR O, ZHANG Tong. Stochastic gradient descent for non-smooth optimization: convergence results and op￾timal averaging schemes[C]//Proceedings of the 30th Inter￾national Conference on International Conference on Ma￾chine Learning. Atlanta, USA, 2013: 1-71−1-79. [9] 陶蔚, 潘志松, 储德军, 等. 使用 Nesterov 步长策略投影 次梯度方法的个体收敛性 [J]. 计算机学报, 2018, 41(1): 164–176. TAO Wei, PAN Zhisong, CHU Dejun, et al. The indi￾vidual convergence of projected subgradient methods us￾ing the Nesterov’s step-size strategy[J]. Chinese journal of computers, 2018, 41(1): 164–176. [10] TAO Wei, PAN Zhisong, WU Gaowei, et al. The strength of Nesterov’s extrapolation in the individual convergence of nonsmooth optimization[J]. IEEE transactions on neur￾al networks and learning systems, 2020, 31(7): [11] 第 6 期 黄鉴之，等：非光滑凸情形 Adam 型算法的最优个体收敛速率 ·1145·