正在加载图片...
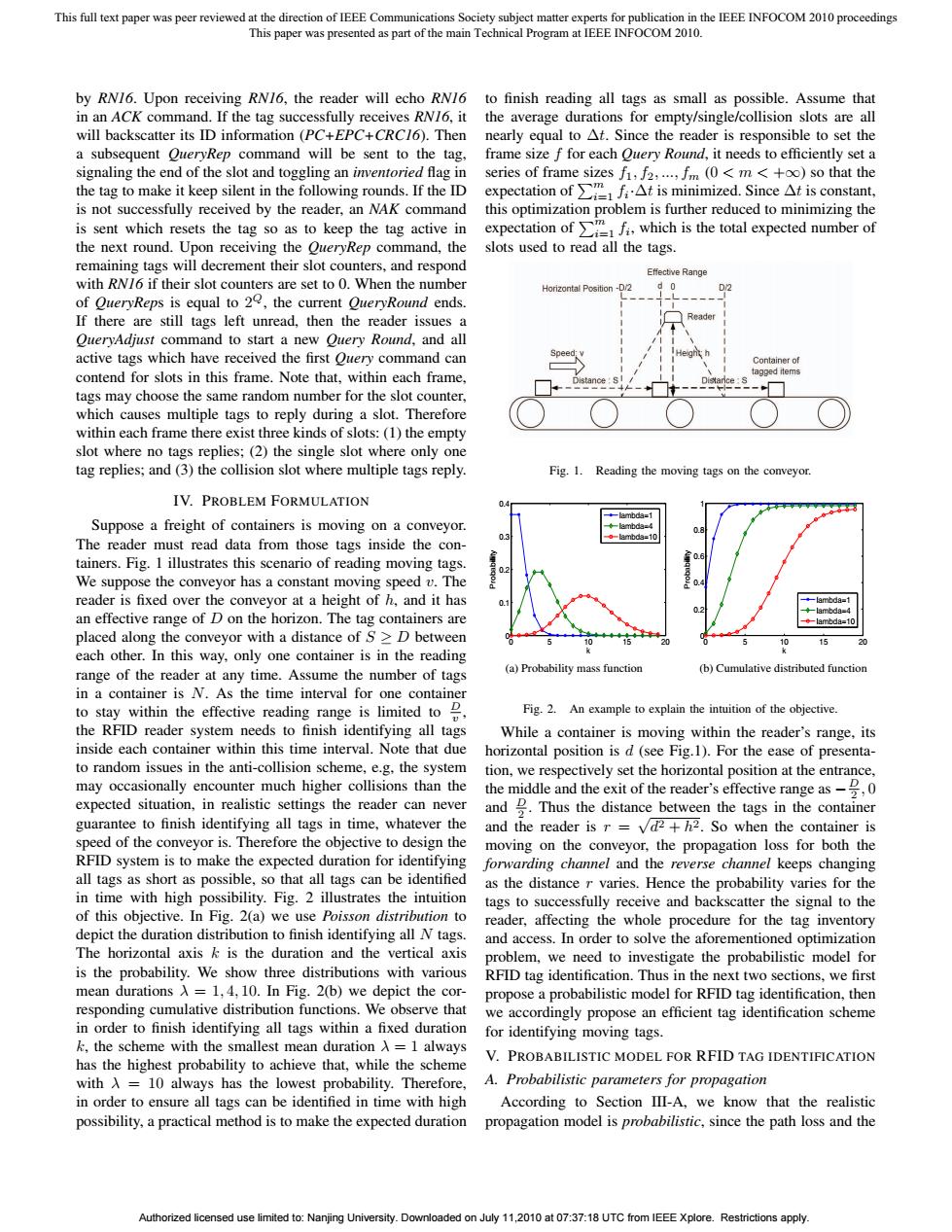
This full text paper was peer reviewed at the direction of IEEE Communications Society subject matter experts for publication in the IEEE INFOCOM 2010 proceedings This paper was presented as part of the main Technical Program at IEEE INFOCOM 2010. by RN16.Upon receiving RN16,the reader will echo RN/6 to finish reading all tags as small as possible.Assume that in an ACK command.If the tag successfully receives RN/6,it the average durations for empty/single/collision slots are all will backscatter its ID information (PC+EPC+CRC/6).Then nearly equal to At.Since the reader is responsible to set the a subsequent OueryRep command will be sent to the tag, frame size f for each Ouery Round,it needs to efficiently set a signaling the end of the slot and toggling an inventoried flag in series of frame sizes f1,f2,...,fm (0<m <+oo)so that the the tag to make it keep silent in the following rounds.If the ID expectation offt is minimized.Since At is constant, is not successfully received by the reader,an NAK command this optimization problem is further reduced to minimizing the is sent which resets the tag so as to keep the tag active in expectation ofwhich is the total expected number of the next round.Upon receiving the OueryRep command,the slots used to read all the tags. remaining tags will decrement their slot counters,and respond Effectve Range with RN/6 if their slot counters are set to 0.When the number Horizontal Position-D/2 d o of QueryReps is equal to 20,the current QueryRound ends. If there are still tags left unread,then the reader issues a QueryAdjust command to start a new Ouery Round,and all active tags which have received the first Query command can Container of contend for slots in this frame.Note that,within each frame, tagged items tags may choose the same random number for the slot counter, which causes multiple tags to reply during a slot.Therefore within each frame there exist three kinds of slots:(1)the empty slot where no tags replies;(2)the single slot where only one tag replies;and (3)the collision slot where multiple tags reply. Fig.1.Reading the moving tags on the conveyor. IV.PROBLEM FORMULATION mbda=1 Suppose a freight of containers is moving on a conveyor. The reader must read data from those tags inside the con- tainers.Fig.I illustrates this scenario of reading moving tags. We suppose the conveyor has a constant moving speed v.The reader is fixed over the conveyor at a height of h,and it has ambda= an effective range of D on the horizon.The tag containers are ◆--lambda=-10 placed along the conveyor with a distance of S>D between 10 15 5 0 each other.In this way,only one container is in the reading (a)Probability mass function range of the reader at any time.Assume the number of tags (b)Cumulative distributed function in a container is N.As the time interval for one container to stay within the effective reading range is limited to Fig.2.An example to explain the intuition of the objective. the RFID reader system needs to finish identifying all tags While a container is moving within the reader's range,its inside each container within this time interval.Note that due horizontal position is d(see Fig.1).For the ease of presenta- to random issues in the anti-collision scheme,e.g,the system tion,we respectively set the horizontal position at the entrance, may occasionally encounter much higher collisions than the the middle and the exit of the reader's effective range as0 expected situation,in realistic settings the reader can never and 2.Thus the distance between the tags in the container guarantee to finish identifying all tags in time,whatever the and the reader is r =vd2+h2.So when the container is speed of the conveyor is.Therefore the objective to design the moving on the conveyor,the propagation loss for both the RFID system is to make the expected duration for identifying forwarding channel and the reverse channel keeps changing all tags as short as possible,so that all tags can be identified as the distance r varies.Hence the probability varies for the in time with high possibility.Fig.2 illustrates the intuition tags to successfully receive and backscatter the signal to the of this objective.In Fig.2(a)we use Poisson distribution to reader,affecting the whole procedure for the tag inventory depict the duration distribution to finish identifying all N tags. and access.In order to solve the aforementioned optimization The horizontal axis k is the duration and the vertical axis problem,we need to investigate the probabilistic model for is the probability.We show three distributions with various RFID tag identification.Thus in the next two sections,we first mean durations A=1,4,10.In Fig.2(b)we depict the cor- propose a probabilistic model for RFID tag identification,then responding cumulative distribution functions.We observe that we accordingly propose an efficient tag identification scheme in order to finish identifying all tags within a fixed duration for identifying moving tags. k,the scheme with the smallest mean duration A =1 always has the highest probability to achieve that,while the scheme V.PROBABILISTIC MODEL FOR RFID TAG IDENTIFICATION with A =10 always has the lowest probability.Therefore, A.Probabilistic parameters for propagation in order to ensure all tags can be identified in time with high According to Section III-A,we know that the realistic possibility,a practical method is to make the expected duration propagation model is probabilistic,since the path loss and the Authorized licensed use limited to:Nanjing University.Downloaded on July 11,2010 at 07:37:18 UTC from IEEE Xplore.Restrictions apply.by RN16. Upon receiving RN16, the reader will echo RN16 in an ACK command. If the tag successfully receives RN16, it will backscatter its ID information (PC+EPC+CRC16). Then a subsequent QueryRep command will be sent to the tag, signaling the end of the slot and toggling an inventoried flag in the tag to make it keep silent in the following rounds. If the ID is not successfully received by the reader, an NAK command is sent which resets the tag so as to keep the tag active in the next round. Upon receiving the QueryRep command, the remaining tags will decrement their slot counters, and respond with RN16 if their slot counters are set to 0. When the number of QueryReps is equal to 2Q, the current QueryRound ends. If there are still tags left unread, then the reader issues a QueryAdjust command to start a new Query Round, and all active tags which have received the first Query command can contend for slots in this frame. Note that, within each frame, tags may choose the same random number for the slot counter, which causes multiple tags to reply during a slot. Therefore within each frame there exist three kinds of slots: (1) the empty slot where no tags replies; (2) the single slot where only one tag replies; and (3) the collision slot where multiple tags reply. IV. PROBLEM FORMULATION Suppose a freight of containers is moving on a conveyor. The reader must read data from those tags inside the containers. Fig. 1 illustrates this scenario of reading moving tags. We suppose the conveyor has a constant moving speed v. The reader is fixed over the conveyor at a height of h, and it has an effective range of D on the horizon. The tag containers are placed along the conveyor with a distance of S ≥ D between each other. In this way, only one container is in the reading range of the reader at any time. Assume the number of tags in a container is N. As the time interval for one container to stay within the effective reading range is limited to D v , the RFID reader system needs to finish identifying all tags inside each container within this time interval. Note that due to random issues in the anti-collision scheme, e.g, the system may occasionally encounter much higher collisions than the expected situation, in realistic settings the reader can never guarantee to finish identifying all tags in time, whatever the speed of the conveyor is. Therefore the objective to design the RFID system is to make the expected duration for identifying all tags as short as possible, so that all tags can be identified in time with high possibility. Fig. 2 illustrates the intuition of this objective. In Fig. 2(a) we use Poisson distribution to depict the duration distribution to finish identifying all N tags. The horizontal axis k is the duration and the vertical axis is the probability. We show three distributions with various mean durations λ = 1, 4, 10. In Fig. 2(b) we depict the corresponding cumulative distribution functions. We observe that in order to finish identifying all tags within a fixed duration k, the scheme with the smallest mean duration λ = 1 always has the highest probability to achieve that, while the scheme with λ = 10 always has the lowest probability. Therefore, in order to ensure all tags can be identified in time with high possibility, a practical method is to make the expected duration to finish reading all tags as small as possible. Assume that the average durations for empty/single/collision slots are all nearly equal to Δt. Since the reader is responsible to set the frame size f for each Query Round, it needs to efficiently set a series of frame sizes f1, f2, ..., fm (0 <m< +∞) so that the expectation of m i=1 fi ·Δt is minimized. Since Δt is constant, this optimization problem is further reduced to minimizing the expectation of m i=1 fi, which is the total expected number of slots used to read all the tags. Fig. 1. Reading the moving tags on the conveyor. 0 5 10 15 20 0 0.1 0.2 0.3 0.4 k Probability lambda=1 lambda=4 lambda=10 0 5 10 15 20 0 0.2 0.4 0.6 0.8 1 k Probability lambda=1 lambda=4 lambda=10 (a) Probability mass function (b) Cumulative distributed function Fig. 2. An example to explain the intuition of the objective. While a container is moving within the reader’s range, its horizontal position is d (see Fig.1). For the ease of presentation, we respectively set the horizontal position at the entrance, the middle and the exit of the reader’s effective range as − D 2 , 0 and D 2 . Thus the distance between the tags in the container and the reader is r = √ d2 + h2. So when the container is moving on the conveyor, the propagation loss for both the forwarding channel and the reverse channel keeps changing as the distance r varies. Hence the probability varies for the tags to successfully receive and backscatter the signal to the reader, affecting the whole procedure for the tag inventory and access. In order to solve the aforementioned optimization problem, we need to investigate the probabilistic model for RFID tag identification. Thus in the next two sections, we first propose a probabilistic model for RFID tag identification, then we accordingly propose an efficient tag identification scheme for identifying moving tags. V. PROBABILISTIC MODEL FOR RFID TAG IDENTIFICATION A. Probabilistic parameters for propagation According to Section III-A, we know that the realistic propagation model is probabilistic, since the path loss and the This full text paper was peer reviewed at the direction of IEEE Communications Society subject matter experts for publication in the IEEE INFOCOM 2010 proceedings This paper was presented as part of the main Technical Program at IEEE INFOCOM 2010. Authorized licensed use limited to: Nanjing University. Downloaded on July 11,2010 at 07:37:18 UTC from IEEE Xplore. Restrictions apply. ��