正在加载图片...
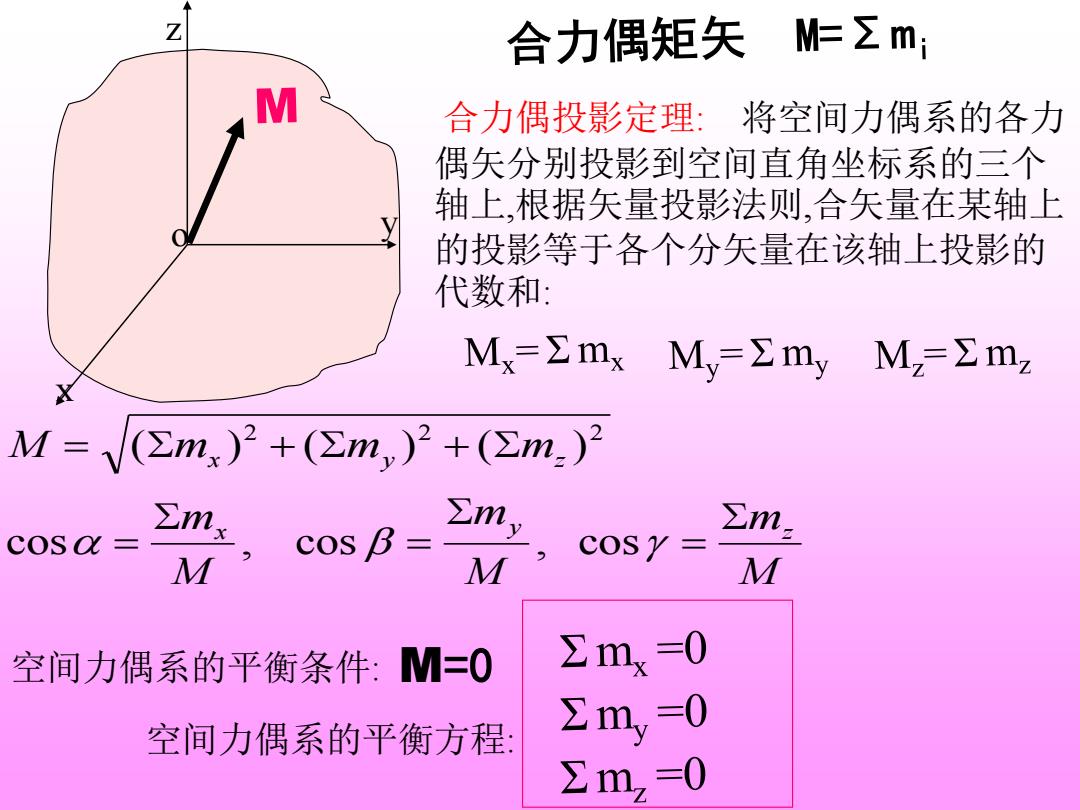
Z 合力偶矩矢 M作Σm; M 合力偶投影定理:将空间力偶系的各力 偶矢分别投影到空间直角坐标系的三个 轴上,根据矢量投影法则,合矢量在某轴上 的投影等于各个分矢量在该轴上投影的 代数和: Mx=∑mxMy=ΣmyMz∑mz M=V(②mx)2+(②m)2+(②m)2 Σmy cosa= cos B= M M M 空间力偶系的平衡条件:M=0 Σmx=0 =0 空间力偶系的平衡方程: Σmy ∑mz =0z y x o 合力偶投影定理: 将空间力偶系的各力 偶矢分别投影到空间直角坐标系的三个 轴上,根据矢量投影法则,合矢量在某轴上 的投影等于各个分矢量在该轴上投影的 代数和: M m M m M m M m m m x y z x y z = = = = + + cos , cos , cos ( ) ( ) ( ) 2 2 2 空间力偶系的平衡条件: M=0 空间力偶系的平衡方程: