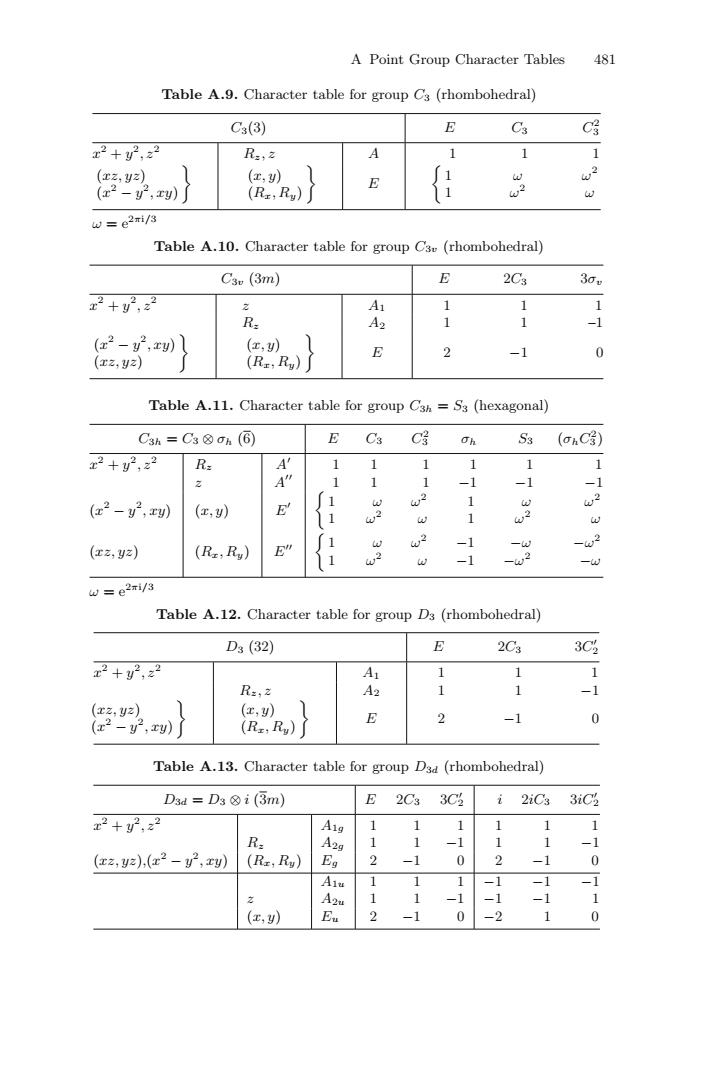
A Point Group Character Tables 481 Table A.9.Character table for group Cs(rhombohedral) C3(3) E Cs C x2+y2,22 R.,2 A 1 1 (xz,yz) (x,y） (x2-2,xy)」 (Rz:Ry) E 1 w2 W e2mi/3 Table A.10.Character table for group C3o(rhombohedral) Csv (3m) E 2C3 30u x2+y,22 A1 1 1 1 R: A2 1 1 -1 (x2-2,x)1】 (x, E 2 -1 0 (x2,y2) (R:;Ru) Table A.11.Character table for group Csh=S3(hexagonal) C3h=C3⑧h(⑥ E Cs c Oh Ss (σhC3) x2+y2,22 R: A 1 1 1 1 1 1 2 A 1 1 1 -1 -1 -1 (x2-2,x) E 1 3 1 w2 (x,y) 1 3 1 3 -1 -w2 (xz,yz) (Rz;Ry) 3 w? -1 -w2 W=e2mi/3 Table A.12.Character table for group Ds(rhombohedral) D3(32) E 2C3 3C2 x2+y2,22 A 1 1 1 R:,2 A2 1 1 -1 (xz,yz) (E,y) (x2-y2,xy) (R=:Ru) E 2 -1 0 Table A.13.Character table for group D3d(rhombohedral) Dsd=Ds⑧i(3m) E 2C3 3C2 2 2iCs 3iC x2+y2,22 Aig 1 1 1 1 1 R: A2g y 1 -1 1 1 -1 (xz,y2),(x2-y2,x (Rz,Ry) Eg 2 -1 0 2 -1 0 Alu 1 1 1 -1 -1 -1 A2u -1 -1 -1 1 (x,y) Eu -1 0 -2 1 0A Point Group Character Tables 481 Table A.9. Character table for group C3 (rhombohedral) C3(3) E C3 C2 3 x2 + y2, z2 Rz, z A 111 (xz, yz) (x2 − y2, xy) " (x, y) (Rx, Ry) " E (1 1 ω ω2 ω2 ω ω = e2πi/3 Table A.10. Character table for group C3v (rhombohedral) C3v (3m) E 2C3 3σv x2 + y2, z2 z A1 1 11 Rz A2 1 1 –1 (x2 − y2, xy) (xz, yz) " (x, y) (Rx, Ry) " E 2 −1 0 Table A.11. Character table for group C3h = S3 (hexagonal) C3h = C3 ⊗ σh (6) E C3 C2 3 σh S3 (σhC2 3 ) x2 + y2, z2 Rz A 11 1 1 1 1 z A 11 1 −1 −1 −1 (x2 − y2, xy) (x, y) E ( 1 1 ω ω2 ω2 ω 1 1 ω ω2 ω2 ω (xz, yz) (Rx, Ry) E ( 1 1 ω ω2 ω2 ω −1 −1 −ω −ω2 −ω2 −ω ω = e2πi/3 Table A.12. Character table for group D3 (rhombohedral) D3 (32) E 2C3 3C 2 x2 + y2, z2 A1 111 Rz, z A2 1 1 −1 (xz, yz) (x2 − y2, xy) " (x, y) (Rx, Ry) " E 2 −1 0 Table A.13. Character table for group D3d (rhombohedral) D3d = D3 ⊗ i (3m) E 2C3 3C 2 i 2iC3 3iC 2 x2 + y2, z2 A1g 111 111 Rz A2g 1 1 −1 1 1 −1 (xz, yz),(x2 − y2, xy) (Rx, Ry) Eg 2 −1 0 2 −1 0 A1u 111 −1 −1 −1 z A2u 1 1 −1 −1 −1 1 (x, y) Eu 2 −1 0 −210