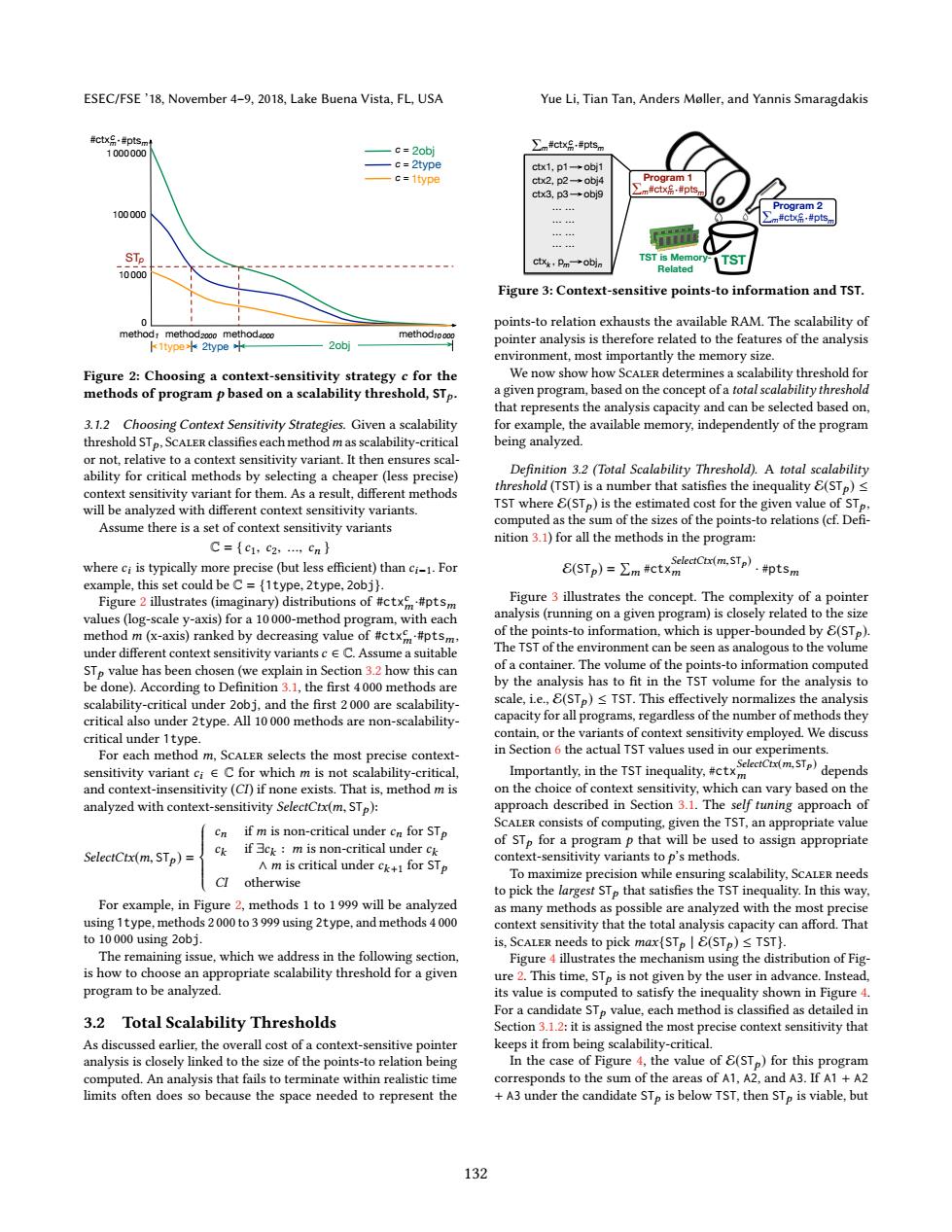
ESEC/FSE'18,November 4-9,2018,Lake Buena Vista,FL,USA Yue Li,Tian Tan,Anders Moller,and Yannis Smaragdakis #ctx#ptsm c=2obj ∑m#ctx号，#ptsn 1000000 -c=2type ctx1,p1→obj1 c=1type ct2,p2→obj4 cbx3,p3-→obj9 Program 2 100000 #ct乐·#pts STp ctxk,Pm→ob TST is Memor 10000 Related Figure 3:Context-sensitive points-to information and TST. 0 points-to relation exhausts the available RAM.The scalability of method methodaooo methodaooo 卡1type2hype中 2obj meth pointer analysis is therefore related to the features of the analysis environment,most importantly the memory size. Figure 2:Choosing a context-sensitivity strategy c for the We now show how SCALER determines a scalability threshold for methods of program p based on a scalability threshold,STp. a given program,based on the concept of a total scalability threshold that represents the analysis capacity and can be selected based on, 3.1.2 Choosing Context Sensitivity Strategies.Given a scalability for example,the available memory,independently of the program threshold STp,ScALER classifies each method m as scalability-critical being analyzed. or not,relative to a context sensitivity variant.It then ensures scal- ability for critical methods by selecting a cheaper (less precise) Definition 3.2 (Total Scalability Threshold).A total scalability context sensitivity variant for them.As a result,different methods threshold(TST)is a number that satisfies the inequality E(STp)< will be analyzed with different context sensitivity variants. TST where E(STp)is the estimated cost for the given value of STp. Assume there is a set of context sensitivity variants computed as the sum of the sizes of the points-to relations(cf.Defi- nition 3.1)for all the methods in the program: C={c1,c2,,cn} where ci is typically more precise(but less efficient)than ci-1.For 8(STp)=∑m#ctxm leeC(,sTp）.ptSm example,this set could be C={1type,2type,2obj). Figure 2 illustrates(imaginary)distributions of #ctx#ptsm Figure 3 illustrates the concept.The complexity of a pointer values (log-scale y-axis)for a 10 000-method program,with each analysis(running on a given program)is closely related to the size method m(x-axis)ranked by decreasing value of #ctxm#ptsm of the points-to information,which is upper-bounded by E(STp). under different context sensitivity variants c e C.Assume a suitable The TST of the environment can be seen as analogous to the volume STp value has been chosen(we explain in Section 3.2 how this can of a container.The volume of the points-to information computed be done).According to Definition 3.1,the first 4000 methods are by the analysis has to fit in the TST volume for the analysis to scalability-critical under 2obj,and the first 2 000 are scalability- scale,i.e.,E(STp)<TST.This effectively normalizes the analysis critical also under 2type.All 10 000 methods are non-scalability- capacity for all programs,regardless of the number of methods they critical under 1 type. contain,or the variants of context sensitivity employed.We discuss For each method m,SCALER selects the most precise context- in Section 6 the actual TST values used in our experiments. sensitivity variant ci E C for which m is not scalability-critical, Importantly the TSTinequality,depends and context-insensitivity(Cl)if none exists.That is,method m is on the choice of context sensitivity,which can vary based on the analyzed with context-sensitivity SelectCtx(m,STp): approach described in Section 3.1.The self tuning approach of Cn if m is non-critical under cn for STp ScALER consists of computing.given the TST,an appropriate value of STp for a program p that will be used to assign appropriate SelectCtx(m,STp)= Ck if 3ck:m is non-critical under ck A m is critical under ck+for STp context-sensitivity variants to p's methods. CI otherwise To maximize precision while ensuring scalability,SCALER needs to pick the largest STp that satisfies the TST inequality.In this way. For example,in Figure 2,methods 1 to 1 999 will be analyzed as many methods as possible are analyzed with the most precise using 1type,methods 2000 to 3 999 using 2type,and methods 4000 context sensitivity that the total analysis capacity can afford.That to 10000 using 2obj. is,SCALER needs to pick max{STp E(STp)s TST}. The remaining issue,which we address in the following section, Figure 4 illustrates the mechanism using the distribution of Fig- is how to choose an appropriate scalability threshold for a given ure 2.This time,STp is not given by the user in advance.Instead, program to be analyzed. its value is computed to satisfy the inequality shown in Figure 4. For a candidate STp value,each method is classified as detailed in 3.2 Total Scalability Thresholds Section 3.1.2:it is assigned the most precise context sensitivity that As discussed earlier,the overall cost of a context-sensitive pointer keeps it from being scalability-critical. analysis is closely linked to the size of the points-to relation being In the case of Figure 4,the value of E(STp)for this program computed.An analysis that fails to terminate within realistic time corresponds to the sum of the areas of A1,A2,and A3.If A1 +A2 limits often does so because the space needed to represent the +A3 under the candidate STp is below TST,then STp is viable,but 132ESEC/FSE ’18, November 4–9, 2018, Lake Buena Vista, FL, USA Yue Li, Tian Tan, Anders Møller, and Yannis Smaragdakis 2type 2obj 0 10 000 ST method 1 method 2000 method 4000 method 10 000 1type 2type 1type 1 000 000 2obj 100 000 p #ctx c m·#pts m c = c = c = Figure 2: Choosing a context-sensitivity strategy c for the methods of program p based on a scalability threshold, STp . 3.1.2 Choosing Context Sensitivity Strategies. Given a scalability threshold STp , Scaler classifies each methodm as scalability-critical or not, relative to a context sensitivity variant. It then ensures scal￾ability for critical methods by selecting a cheaper (less precise) context sensitivity variant for them. As a result, different methods will be analyzed with different context sensitivity variants. Assume there is a set of context sensitivity variants C = { c1, c2, ..., cn } where ci is typically more precise (but less efficient) than ci−1. For example, this set could be C = {1type, 2type, 2obj}. Figure 2 illustrates (imaginary) distributions of #ctxc m·#ptsm values (log-scale y-axis) for a 10 000-method program, with each method m (x-axis) ranked by decreasing value of #ctxc m·#ptsm, under different context sensitivity variantsc ∈ C. Assume a suitable STp value has been chosen (we explain in Section 3.2 how this can be done). According to Definition 3.1, the first 4 000 methods are scalability-critical under 2obj, and the first 2 000 are scalability￾critical also under 2type. All 10 000 methods are non-scalability￾critical under 1type. For each method m, Scaler selects the most precise context￾sensitivity variant ci ∈ C for which m is not scalability-critical, and context-insensitivity (CI) if none exists. That is, method m is analyzed with context-sensitivity SelectCtx(m, STp ): SelectCtx(m, STp ) =    cn if m is non-critical under cn for STp ck if ∃ck : m is non-critical under ck ∧ m is critical under ck+1 for STp CI otherwise For example, in Figure 2, methods 1 to 1 999 will be analyzed using 1type, methods 2 000 to 3 999 using 2type, and methods 4 000 to 10 000 using 2obj. The remaining issue, which we address in the following section, is how to choose an appropriate scalability threshold for a given program to be analyzed. 3.2 Total Scalability Thresholds As discussed earlier, the overall cost of a context-sensitive pointer analysis is closely linked to the size of the points-to relation being computed. An analysis that fails to terminate within realistic time limits often does so because the space needed to represent the TST is Memory- TST Related ctx1, p1 obj1 ctx2, p2 obj4 ctx3, p3 obj9 ctx , p obj k m n … … … … … … … … Program 1 Program 2 #ctx c Σm m·#pts m #ctx c Σm m·#pts m #ctx c Σm m·#pts m Figure 3: Context-sensitive points-to information and TST. points-to relation exhausts the available RAM. The scalability of pointer analysis is therefore related to the features of the analysis environment, most importantly the memory size. We now show how Scaler determines a scalability threshold for a given program, based on the concept of a total scalability threshold that represents the analysis capacity and can be selected based on, for example, the available memory, independently of the program being analyzed. Definition 3.2 (Total Scalability Threshold). A total scalability threshold (TST) is a number that satisfies the inequality E(STp ) ≤ TST where E(STp ) is the estimated cost for the given value of STp , computed as the sum of the sizes of the points-to relations (cf. Defi￾nition 3.1) for all the methods in the program: E(STp ) = Í m #ctx SelectCtx(m,STp ) m · #ptsm Figure 3 illustrates the concept. The complexity of a pointer analysis (running on a given program) is closely related to the size of the points-to information, which is upper-bounded by E(STp ). The TST of the environment can be seen as analogous to the volume of a container. The volume of the points-to information computed by the analysis has to fit in the TST volume for the analysis to scale, i.e., E(STp ) ≤ TST. This effectively normalizes the analysis capacity for all programs, regardless of the number of methods they contain, or the variants of context sensitivity employed. We discuss in Section 6 the actual TST values used in our experiments. Importantly, in the TST inequality, #ctx SelectCtx(m,STp ) m depends on the choice of context sensitivity, which can vary based on the approach described in Section 3.1. The self tuning approach of Scaler consists of computing, given the TST, an appropriate value of STp for a program p that will be used to assign appropriate context-sensitivity variants to p’s methods. To maximize precision while ensuring scalability, Scaler needs to pick the largest STp that satisfies the TST inequality. In this way, as many methods as possible are analyzed with the most precise context sensitivity that the total analysis capacity can afford. That is, Scaler needs to pick max{STp | E(STp ) ≤ TST}. Figure 4 illustrates the mechanism using the distribution of Fig￾ure 2. This time, STp is not given by the user in advance. Instead, its value is computed to satisfy the inequality shown in Figure 4. For a candidate STp value, each method is classified as detailed in Section 3.1.2: it is assigned the most precise context sensitivity that keeps it from being scalability-critical. In the case of Figure 4, the value of E(STp ) for this program corresponds to the sum of the areas of A1, A2, and A3. If A1 + A2 + A3 under the candidate STp is below TST, then STp is viable, but 132