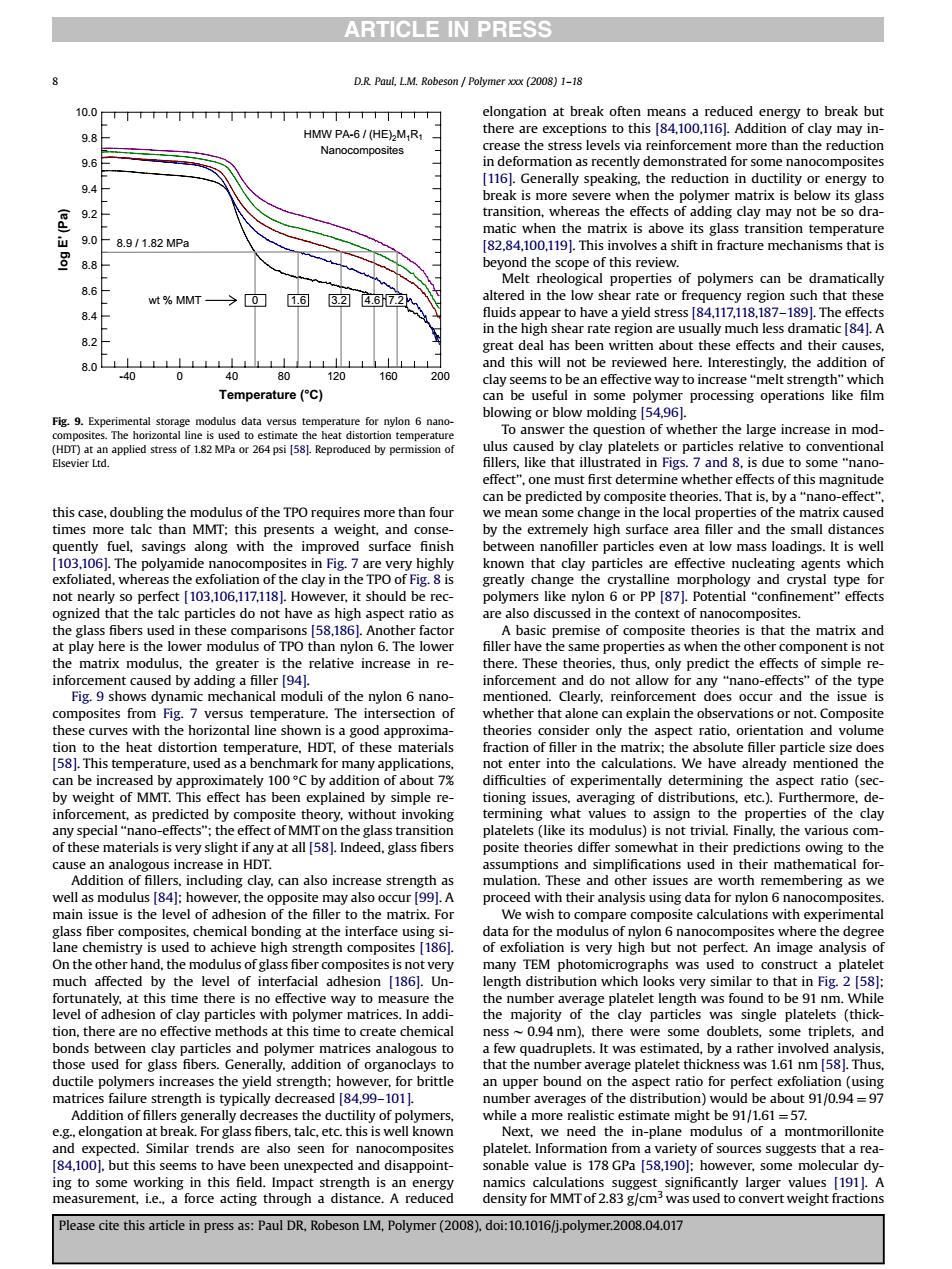
ARTICLE IN PRESS r2008)1-18 o break bu there are exc than the [16 whe th reduction n dc 92 thes the ef of ad clay may be so 8.91182MPa 8.8 ar to l 82 o0.400010 200 here.Inter Temperature (C) r processing operations like film Fig.9.Exp the question of whether the large increase in mod to some "nar That is the an som exfoliat the clay in the gre nge ticles do not have are relative increase in re These t dict the ef ur horizontal line show rature.used asa benchmark for We have alr eady n the mple posite theore iffer s ease strength and her h the ssue is the n of th to the matrix.For e pare composite calculations withe imenta 4 nm)ther ere some doubl ome triplets,and mb age platelet thi 1.6 is typically decreased of the distribution) about91/0.94=97 reak.For while a need th are also Please cite this article in press as:Paul DR,Robeson LM,Polymer(2008).doi:10.1016/j.polymer.2008.04.017this case, doubling the modulus of the TPO requires more than four times more talc than MMT; this presents a weight, and conse￾quently fuel, savings along with the improved surface finish [103,106]. The polyamide nanocomposites in Fig. 7 are very highly exfoliated, whereas the exfoliation of the clay in the TPO of Fig. 8 is not nearly so perfect [103,106,117,118]. However, it should be rec￾ognized that the talc particles do not have as high aspect ratio as the glass fibers used in these comparisons [58,186]. Another factor at play here is the lower modulus of TPO than nylon 6. The lower the matrix modulus, the greater is the relative increase in re￾inforcement caused by adding a filler [94]. Fig. 9 shows dynamic mechanical moduli of the nylon 6 nano￾composites from Fig. 7 versus temperature. The intersection of these curves with the horizontal line shown is a good approxima￾tion to the heat distortion temperature, HDT, of these materials [58]. This temperature, used as a benchmark for many applications, can be increased by approximately 100 C by addition of about 7% by weight of MMT. This effect has been explained by simple re￾inforcement, as predicted by composite theory, without invoking any special ‘‘nano-effects’’; the effect of MMT on the glass transition of these materials is very slight if any at all [58]. Indeed, glass fibers cause an analogous increase in HDT. Addition of fillers, including clay, can also increase strength as well as modulus [84]; however, the opposite may also occur [99]. A main issue is the level of adhesion of the filler to the matrix. For glass fiber composites, chemical bonding at the interface using si￾lane chemistry is used to achieve high strength composites [186]. On the other hand, the modulus of glass fiber composites is not very much affected by the level of interfacial adhesion [186]. Un￾fortunately, at this time there is no effective way to measure the level of adhesion of clay particles with polymer matrices. In addi￾tion, there are no effective methods at this time to create chemical bonds between clay particles and polymer matrices analogous to those used for glass fibers. Generally, addition of organoclays to ductile polymers increases the yield strength; however, for brittle matrices failure strength is typically decreased [84,99–101]. Addition of fillers generally decreases the ductility of polymers, e.g., elongation at break. For glass fibers, talc, etc. this is well known and expected. Similar trends are also seen for nanocomposites [84,100], but this seems to have been unexpected and disappoint￾ing to some working in this field. Impact strength is an energy measurement, i.e., a force acting through a distance. A reduced elongation at break often means a reduced energy to break but there are exceptions to this [84,100,116]. Addition of clay may in￾crease the stress levels via reinforcement more than the reduction in deformation as recently demonstrated for some nanocomposites [116]. Generally speaking, the reduction in ductility or energy to break is more severe when the polymer matrix is below its glass transition, whereas the effects of adding clay may not be so dra￾matic when the matrix is above its glass transition temperature [82,84,100,119]. This involves a shift in fracture mechanisms that is beyond the scope of this review. Melt rheological properties of polymers can be dramatically altered in the low shear rate or frequency region such that these fluids appear to have a yield stress [84,117,118,187–189]. The effects in the high shear rate region are usually much less dramatic [84]. A great deal has been written about these effects and their causes, and this will not be reviewed here. Interestingly, the addition of clay seems to be an effective way to increase ‘‘melt strength’’ which can be useful in some polymer processing operations like film blowing or blow molding [54,96]. To answer the question of whether the large increase in mod￾ulus caused by clay platelets or particles relative to conventional fillers, like that illustrated in Figs. 7 and 8, is due to some ‘‘nano￾effect’’, one must first determine whether effects of this magnitude can be predicted by composite theories. That is, by a ‘‘nano-effect’’, we mean some change in the local properties of the matrix caused by the extremely high surface area filler and the small distances between nanofiller particles even at low mass loadings. It is well known that clay particles are effective nucleating agents which greatly change the crystalline morphology and crystal type for polymers like nylon 6 or PP [87]. Potential ‘‘confinement’’ effects are also discussed in the context of nanocomposites. A basic premise of composite theories is that the matrix and filler have the same properties as when the other component is not there. These theories, thus, only predict the effects of simple re￾inforcement and do not allow for any ‘‘nano-effects’’ of the type mentioned. Clearly, reinforcement does occur and the issue is whether that alone can explain the observations or not. Composite theories consider only the aspect ratio, orientation and volume fraction of filler in the matrix; the absolute filler particle size does not enter into the calculations. We have already mentioned the difficulties of experimentally determining the aspect ratio (sec￾tioning issues, averaging of distributions, etc.). Furthermore, de￾termining what values to assign to the properties of the clay platelets (like its modulus) is not trivial. Finally, the various com￾posite theories differ somewhat in their predictions owing to the assumptions and simplifications used in their mathematical for￾mulation. These and other issues are worth remembering as we proceed with their analysis using data for nylon 6 nanocomposites. We wish to compare composite calculations with experimental data for the modulus of nylon 6 nanocomposites where the degree of exfoliation is very high but not perfect. An image analysis of many TEM photomicrographs was used to construct a platelet length distribution which looks very similar to that in Fig. 2 [58]; the number average platelet length was found to be 91 nm. While the majority of the clay particles was single platelets (thick￾ness w 0.94 nm), there were some doublets, some triplets, and a few quadruplets. It was estimated, by a rather involved analysis, that the number average platelet thickness was 1.61 nm [58]. Thus, an upper bound on the aspect ratio for perfect exfoliation (using number averages of the distribution) would be about 91/0.94 ¼ 97 while a more realistic estimate might be 91/1.61 ¼57. Next, we need the in-plane modulus of a montmorillonite platelet. Information from a variety of sources suggests that a rea￾sonable value is 178 GPa [58,190]; however, some molecular dy￾namics calculations suggest significantly larger values [191]. A density for MMT of 2.83 g/cm3 was used to convert weight fractions -40 0 40 80 120 160 200 log E' (Pa) 8.0 8.2 8.4 8.6 8.8 9.0 9.2 9.4 9.6 9.8 10.0 Temperature (°C) HMW PA-6 / (HE)2M1R1 Nanocomposites wt % MMT 0 1.6 3.2 4.6 7.2 8.9 / 1.82 MPa Fig. 9. Experimental storage modulus data versus temperature for nylon 6 nano￾composites. The horizontal line is used to estimate the heat distortion temperature (HDT) at an applied stress of 1.82 MPa or 264 psi [58]. Reproduced by permission of Elsevier Ltd. 8 D.R. Paul, L.M. Robeson / Polymer xxx (2008) 1–18 ARTICLE IN PRESS Please cite this article in press as: Paul DR, Robeson LM, Polymer (2008), doi:10.1016/j.polymer.2008.04.017