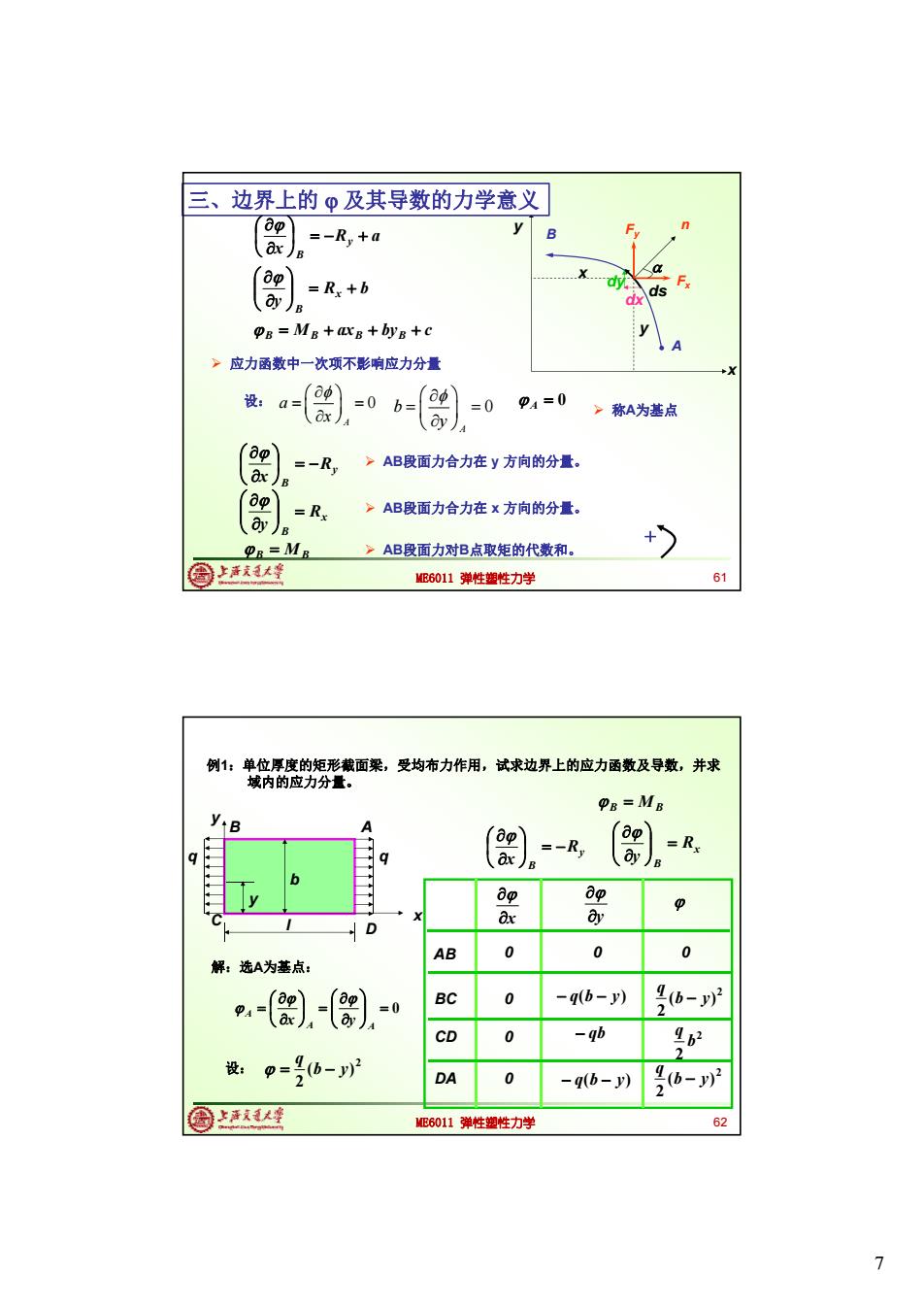
三、边界上的φ及其导数的力学意义 ap x)B =-R,+a y B ap a =Rx+b d )B ds dx PB=MB+axg +byg+c y >应力函数中一次项不影响应力分量 X 设：a= =0p4=0 ax =0b= y >称A为基点 bp =-R >AB段面力合力在y方向的分量。 ax)B bp ~AB段面力合力在x方向的分量。 B =Rx + R=MR 》AB段面力对B点取矩的代数和。 上活大峰 ME6011弹性塑性力学 61 例1：单位厚度的矩形截面梁，受均布力作用，试求边界上的应力函数及导数，并求 域内的应力分量。 PB=MB yB A ap 8p =Rx 9 ax =-Ry B B 6 bp op X Ox D AB 0 0 0 解：选A为基点： -()- BC 0 -q(b-y) 是0-3 CD 0 -qb 4b2 设： p=是b-2 DA q(b-y) 4b-y)2 国上清大峰 ME6011弹性塑性力学 62 77 ME6011 弹性塑性力学 M ax by c  B  B  B  B  R b y x B             Fx Fy n A B dx dy ds  x y x y 三、边界上的 及其导数的力学意义 R a x y B            0 A a x           设： 0 A b y            0  A  应力函数中一次项不影响应力分量  称A为基点 y B R x            AB段面力合力在 y 方向的分量。 x B R y             AB段面力合力在 x 方向的分量。  B  MB  AB段面力对B点取矩的代数和。 ＋ 61 ME6011 弹性塑性力学 例1：单位厚度的矩形截面梁，受均布力作用，试求边界上的应力函数及导数，并求 域内的应力分量。 x y C l q y B A D q b 解：选A为基点：  0                     A A A x y    y B R x           x B R y             B  MB AB BC CD DA x  y   000 0 0 0  q(b  y)  qb  q(b  y) 2 ( ) 2 b y q  2 ( ) 2 b y q  2 2 b q 2 ( ) 2 b y q 设：    62