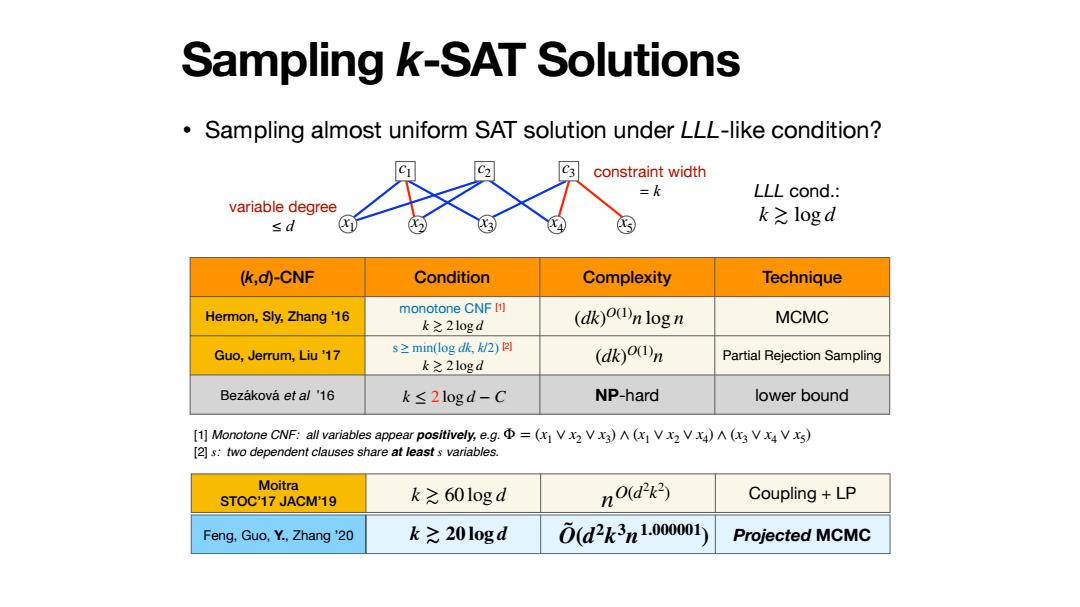
Sampling k-SAT Solutions Sampling almost uniform SAT solution under LLL-like condition? constraint width =k LLL cond.: variable degree sd k之logd (k,d)-CNF Condition Complexity Technique Hermon,Sly,Zhang'16 monotone CNF [1] k之21ogd (dk)o(n log n MCMC Guo,Jerrum,Liu'17 s≥min(log dk/2)☒ (dk)o(n Partial Rejection Sampling k之21ogd Bezakova et al '16 k≤2logd-C NP-hard lower bound [1]Monotone CNF:all variables appear positively,e.g.=(x V2 VX)(x VX2Vx)A (x3 Vx V xs) [2]s:two dependent clauses share at least s variables. Moitra STOC'17 JACM'19 k之60logd nO(dk) Coupling LP Feng,Guo,Y.,Zhang'20 k之20logd 0(d2k3n1.000001 Projected MCMC• Sampling almost uniform SAT solution under LLL-like condition? Sampling k-SAT Solutions (k,d)-CNF Condition Complexity Technique Hermon, Sly, Zhang ’16 monotone CNF [1] MCMC Guo, Jerrum, Liu ’17 s ≥ min(log dk, k/2) [2] Partial Rejection Sampling Bezáková et al ’16 NP-hard lower bound k ≳ 2 log d (dk) O(1) n log n k ≳ 2 log d (dk) O(1) n k ≤ 2 log d − C [1] Monotone CNF: all variables appear positively, e.g. [2] s: two dependent clauses share at least 𝑠 variables. Φ = (x1 ∨ x2 ∨ x3) ∧ (x1 ∨ x2 ∨ x4) ∧ (x3 ∨ x4 ∨ x5) Moitra STOC’17 JACM’19 k ≳ 60 log d Coupling + LP nO(d2 k2 ) Feng, Guo, Y., Zhang ’20 k ≳ 20 log d O ˜ (d2k3 n1.000001) Projected MCMC c1 c2 c3 x1 x2 x3 x4 x5 constraint width = k variable degree ≤ d LLL cond.: k ≳ log d