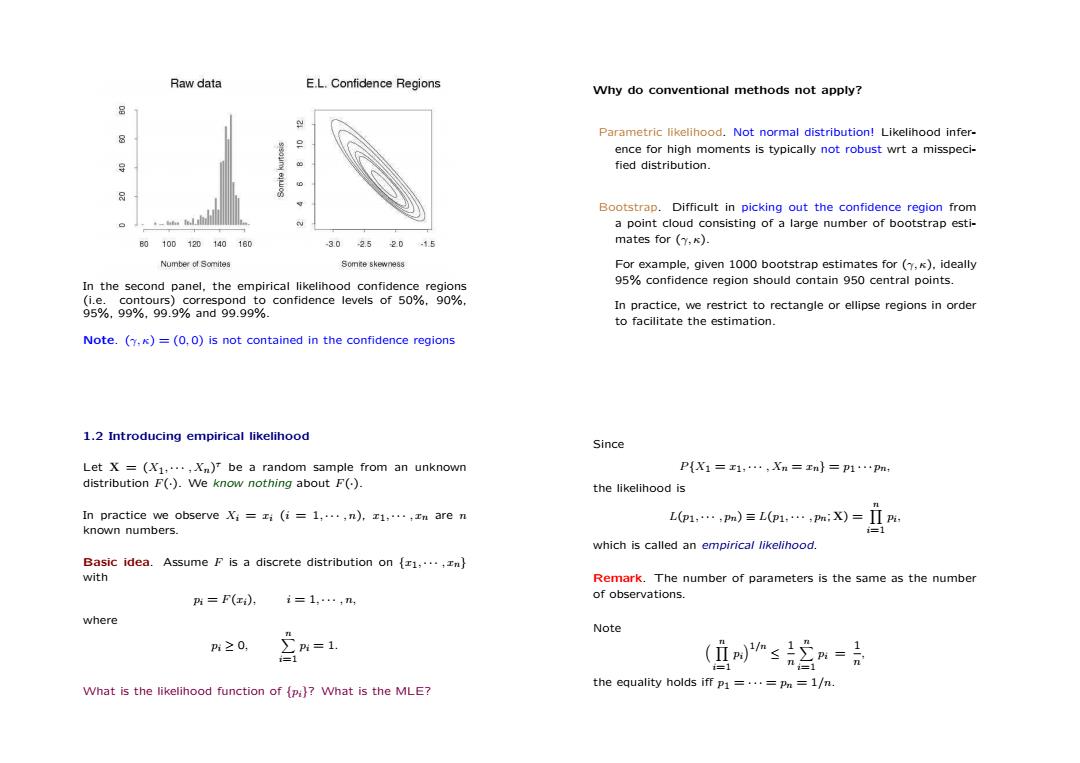
Raw data E.L.Confidence Regions Why do conventional methods not apply? Parametric likelihood.Not normal distribution!Likelihood infer- ence for high moments is typically not robust wrt a misspeci- 导 fied distribution. 8 Bootstrap.Difficult in picking out the confidence region from a point cloud consisting of a large number of bootstrap esti- E0100120140160 3.02.5.201.5 mates for (,) Number of Somites Somte skewness For example,given 1000 bootstrap estimates for (y,K),ideally In the second panel,the empirical likelihood confidence regions 95%confidence region should contain 950 central points. (i.e.contours)correspond to confidence levels of 50%,90%, In practice,we restrict to rectangle or ellipse regions in order 95%,99%,99.9%and99.99% to facilitate the estimation. Note.(y.K)=(0,0)is not contained in the confidence regions 1.2 Introducing empirical likelihood Since Let X =(X1,...,Xn)be a random sample from an unknown P{X1=r1,…,Xn=n}=p1…p distribution F().We know nothing about F(). the likelihood is In practice we observeXi=i (i 1,...,n),z1,...;In are n L(p1,,Pm）三L(p1,…,pmX)=Π， known numbers. 1=1 which is called an empirical likelihood. Basic idea.Assume F is a discrete distribution on1,..,n with Remark.The number of parameters is the same as the number Pi=F(ri), i=1,…,n of observations. where Note P≥0， 含州=1 =1 n=1 What is the likelihood function of(pi)?What is the MLE? the equality holds iff p1=...=Pn 1/n.In the second panel, the empirical likelihood confidence regions (i.e. contours) correspond to confidence levels of 50%, 90%, 95%, 99%, 99.9% and 99.99%. Note. (γ, κ) = (0, 0) is not contained in the confidence regions Why do conventional methods not apply? Parametric likelihood. Not normal distribution! Likelihood infer￾ence for high moments is typically not robust wrt a misspeci- fied distribution. Bootstrap. Difficult in picking out the confidence region from a point cloud consisting of a large number of bootstrap esti￾mates for (γ, κ). For example, given 1000 bootstrap estimates for (γ, κ), ideally 95% confidence region should contain 950 central points. In practice, we restrict to rectangle or ellipse regions in order to facilitate the estimation. 1.2 Introducing empirical likelihood Let X = (X1, · · · , Xn) τ be a random sample from an unknown distribution F(·). We know nothing about F(·). In practice we observe Xi = xi (i = 1, · · · , n), x1, · · · , xn are n known numbers. Basic idea. Assume F is a discrete distribution on {x1, · · · , xn} with pi = F(xi), i = 1, · · · , n, where pi ≥ 0, Xn i=1 pi = 1. What is the likelihood function of {pi}? What is the MLE? Since P{X1 = x1, · · · , Xn = xn} = p1 · · · pn, the likelihood is L(p1, · · · , pn) ≡ L(p1, · · · , pn; X) = Yn i=1 pi , which is called an empirical likelihood. Remark. The number of parameters is the same as the number of observations. Note  Yn i=1 pi 1/n ≤ 1 n Xn i=1 pi = 1 n , the equality holds iff p1 = · · · = pn = 1/n