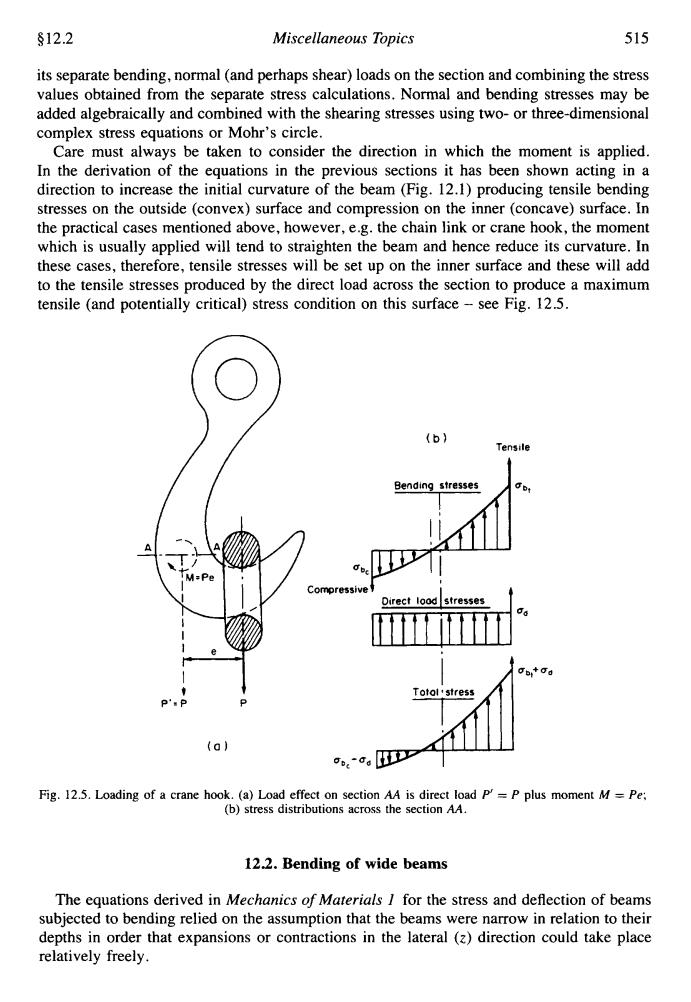
§12.2 Miscellaneous Topics 515 its separate bending,normal(and perhaps shear)loads on the section and combining the stress values obtained from the separate stress calculations.Normal and bending stresses may be added algebraically and combined with the shearing stresses using two-or three-dimensional complex stress equations or Mohr's circle. Care must always be taken to consider the direction in which the moment is applied. In the derivation of the equations in the previous sections it has been shown acting in a direction to increase the initial curvature of the beam(Fig.12.1)producing tensile bending stresses on the outside (convex)surface and compression on the inner (concave)surface.In the practical cases mentioned above,however,e.g.the chain link or crane hook,the moment which is usually applied will tend to straighten the beam and hence reduce its curvature.In these cases,therefore,tensile stresses will be set up on the inner surface and these will add to the tensile stresses produced by the direct load across the section to produce a maximum tensile (and potentially critical)stress condition on this surface-see Fig.12.5. (b) Tensile Bending stresses 6 Pe Compressive Direct lood stresses 60 Totol stress A. (a) ,c。DD Fig.12.5.Loading of a crane hook.(a)Load effect on section AA is direct load P'=P plus moment M=Pe: (b)stress distributions across the section AA. 12.2.Bending of wide beams The equations derived in Mechanics of Materials I for the stress and deflection of beams subjected to bending relied on the assumption that the beams were narrow in relation to their depths in order that expansions or contractions in the lateral (z)direction could take place relatively freely.$12.2 Miscellaneous Topics 515 its separate bending, normal (and perhaps shear) loads on the section and combining the stress values obtained from the separate stress calculations. Normal and bending stresses may be added algebraically and combined with the shearing stresses using two- or three-dimensional complex stress equations or Mohr's circle. Care must always be taken to consider the direction in which the moment is applied. In the derivation of the equations in the previous sections it has been shown acting in a direction to increase the initial curvature of the beam (Fig. 12.1) producing tensile bending stresses on the outside (convex) surface and compression on the inner (concave) surface. In the practical cases mentioned above, however, e.g. the chain link or crane hook, the moment which is usually applied will tend to straighten the beam and hence reduce its curvature. In these cases, therefore, tensile stresses will be set up on the inner surface and these will add to the tensile stresses produced by the direct load across the section to produce a maximum tensile (and potentially critical) stress condition on this surface - see Fig. 12.5. P': P t 1 P Fig. 12.5. Loading of a crane hook. (a) Load effect on section AA is direct load P' = P plus moment M = Pe; (b) stress distributions across the section AA. 12.2. Bending of wide beams The equations derived in Mechanics of Materials 1 for the stress and deflection of beams subjected to bending relied on the assumption that the beams were narrow in relation to their depths in order that expansions or contractions in the lateral (2) direction could take place relatively freely