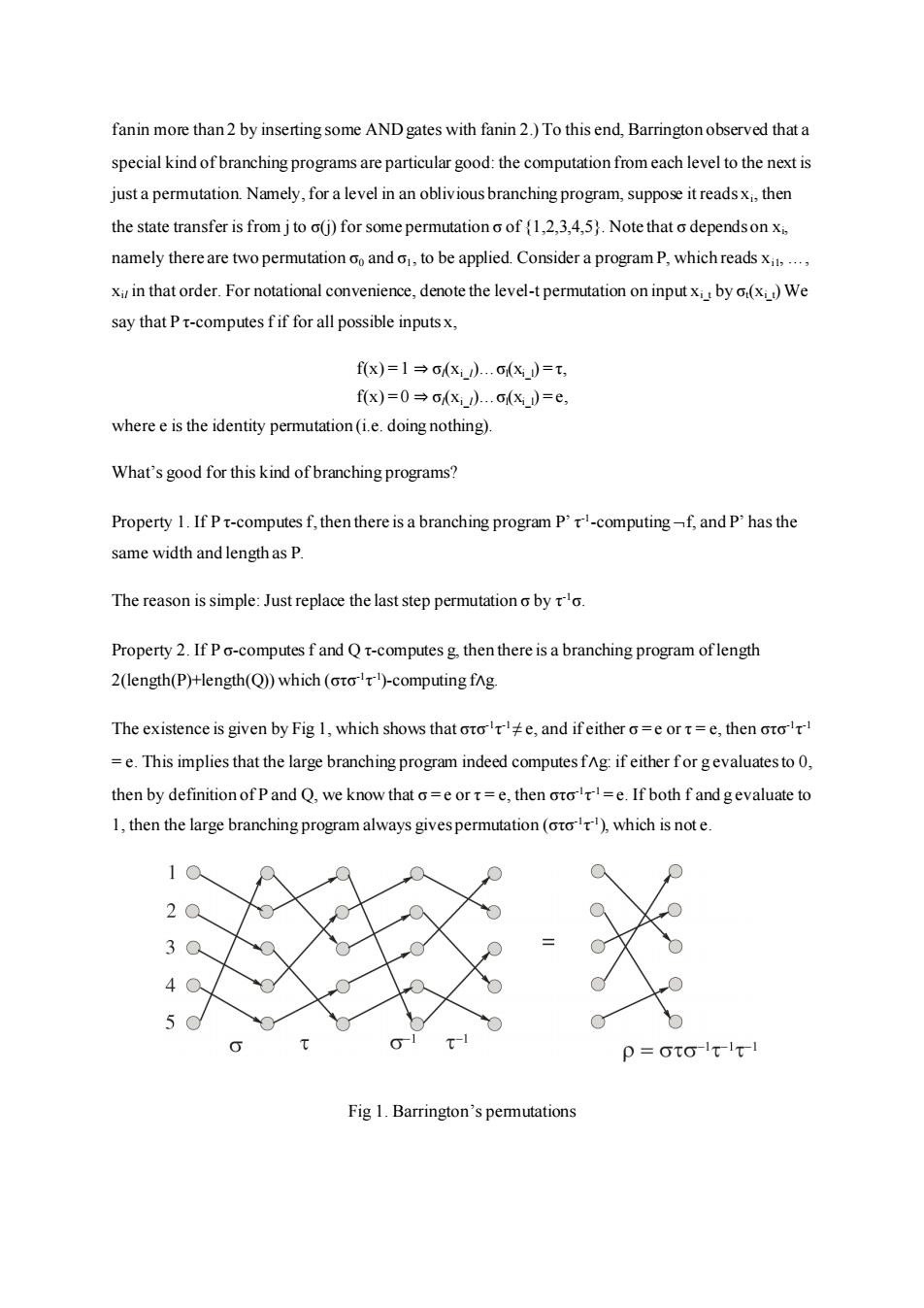
fanin more than 2 by inserting some AND gates with fanin 2.)To this end,Barrington observed that a special kind of branching programs are particular good:the computation from each level to the next is just a permutation.Namely,for a level in an oblivious branching program,suppose it reads xi,then the state transfer is from j to o(j)for some permutation o of (1,2,3,4,5).Note that o dependson xi, namely there are two permutation oo ando,to be applied.Consider a program P,which readsx,.., xi in that order.For notational convenience,denote the level-t permutation on input x by o(x)We say that P t-computes f if for all possible inputsx, fx)=1→(x).X)=t, fx)=0→oxd.c(x)=e, where e is the identity permutation(i.e.doing nothing). What's good for this kind of branching programs? Property 1.If Pt-computes f,then there is a branching program P't-computing-f,and P'has the same width and length as P. The reason is simple:Just replace the last step permutation o by o. Property 2.If P o-computes f and Q t-computes g,then there is a branching program oflength 2(length(P)+length(Q))which(oro)-computing fng The existence is given by Fig 1,which shows that ote,and ifeither o=e or t=e,then oto =e.This implies that the large branching program indeed computes fAg:if either for gevaluates to 0, then by definition of P and Q,we know that o=e or t=e,then oro=e.If both f and gevaluate to 1,then the large branching program always gives permutation(oto),which is not e. p=oto-lt-it-1 Fig 1.Barrington's permutationsfanin more than 2 by inserting some AND gates with fanin 2.) To this end, Barrington observed that a special kind of branching programs are particular good: the computation from each level to the next is just a permutation. Namely, for a level in an oblivious branching program, suppose it reads xi , then the state transfer is from j to σ(j) for some permutation σ of {1,2,3,4,5}. Note that σ depends on xi , namely there are two permutation σ0 and σ1, to be applied. Consider a program P, which reads xi1, …, xil in that order. For notational convenience, denote the level-t permutation on input xi_t by σt(xi_t) We say that P τ-computes f if for all possible inputs x, f(x) = 1 ⇒ σl(xi_l)…σl(xi_l) = τ, f(x) = 0 ⇒ σl(xi_l)…σl(xi_l) = e, where e is the identity permutation (i.e. doing nothing). What’s good for this kind of branching programs? Property 1. If P τ-computes f, then there is a branching program P’ τ -1 -computing f, and P’ has the same width and length as P. The reason is simple: Just replace the last step permutation σ by τ -1σ. Property 2. If P σ-computes f and Q τ-computes g, then there is a branching program of length 2(length(P)+length(Q)) which (στσ -1 τ -1 )-computing f∧g. The existence is given by Fig 1, which shows that στσ -1 τ -1≠ e, and if either σ = e or τ = e, then στσ -1 τ -1 = e. This implies that the large branching program indeed computes f∧g: if either f or g evaluates to 0, then by definition of P and Q, we know that σ = e or τ = e, then στσ -1 τ -1 = e. If both f and g evaluate to 1, then the large branching program always gives permutation (στσ -1 τ -1 ), which is not e. Fig 1. Barrington’s permutations