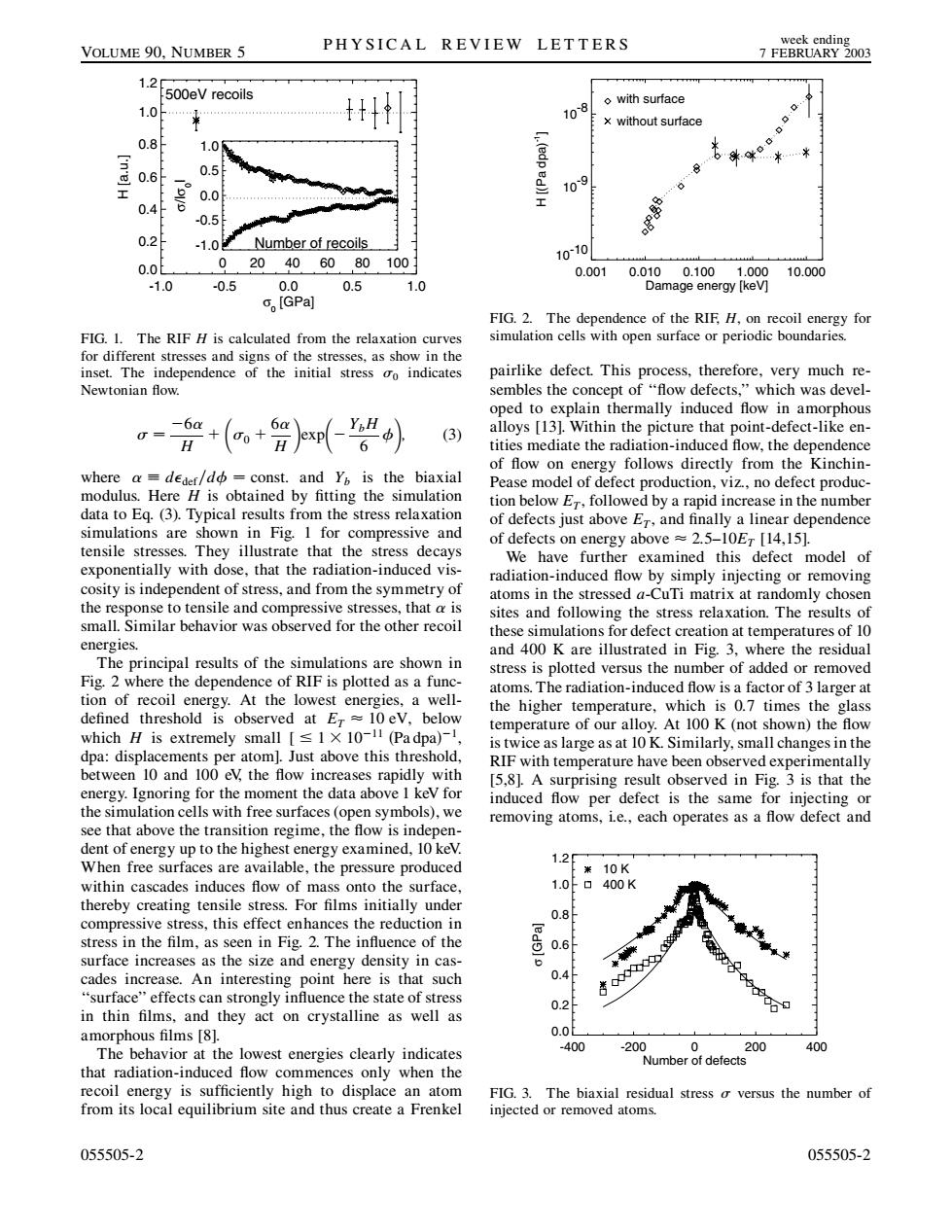
week ending VOLUME 90.NUMBER 5 PHYSICAL REVIEW LETTERS 7 FEBRUARY 2003 1.2 500eV recoils o with surface 108 x without surface 0.8 1.0 (edp 0.6 0.5 工 0.0 109 0.4 6 -0.5 0.2 -1.0 Number of recoils 0 204060801001 10~10 0.0 0.001 0.0100.1001.000 10.000 -1.0 -0.5 0.0 0.5 1.0 Damage energy [keV] [GPa] FIG.2.The dependence of the RIF,H,on recoil energy for FIG.1. The RIF H is calculated from the relaxation curves simulation cells with open surface or periodic boundaries. for different stresses and signs of the stresses,as show in the inset.The independence of the initial stress oo indicates pairlike defect.This process,therefore,very much re- Newtonian flow. sembles the concept of "flow defects,"which was devel- oped to explain thermally induced flow in amorphous 0=- +(+- (3) alloys [13].Within the picture that point-defect-like en- tities mediate the radiation-induced flow,the dependence of flow on energy follows directly from the Kinchin- where a deder/do const.and Y is the biaxial Pease model of defect production,viz.,no defect produc- modulus.Here H is obtained by fitting the simulation tion below Er,followed by a rapid increase in the number data to Eq.(3).Typical results from the stress relaxation of defects just above Er,and finally a linear dependence simulations are shown in Fig.I for compressive and of defects on energy above =2.5-10ET [14,15]. tensile stresses.They illustrate that the stress decays We have further examined this defect model of exponentially with dose,that the radiation-induced vis- radiation-induced flow by simply injecting or removing cosity is independent of stress,and from the symmetry of atoms in the stressed a-CuTi matrix at randomly chosen the response to tensile and compressive stresses,that a is sites and following the stress relaxation.The results of small.Similar behavior was observed for the other recoil these simulations for defect creation at temperatures of 10 energies. and 400 K are illustrated in Fig.3,where the residual The principal results of the simulations are shown in stress is plotted versus the number of added or removed Fig.2 where the dependence of RIF is plotted as a func- atoms.The radiation-induced flow is a factor of 3 larger at tion of recoil energy.At the lowest energies,a well- the higher temperature,which is 0.7 times the glass defined threshold is observed at Er10 ev,below temperature of our alloy.At 100 K(not shown)the flow which H is extremely small 1 X 10-11(Padpa)-1 is twice as large as at 10 K.Similarly,small changes in the dpa:displacements per atom].Just above this threshold, RIF with temperature have been observed experimentally between 10 and 100 ev,the flow increases rapidly with [5,8].A surprising result observed in Fig.3 is that the energy.Ignoring for the moment the data above I keV for induced flow per defect is the same for injecting or the simulation cells with free surfaces (open symbols),we removing atoms,ie.,each operates as a flow defect and see that above the transition regime,the flow is indepen- dent of energy up to the highest energy examined,10 keV. 1.2「 When free surfaces are available,the pressure produced 米10K within cascades induces flow of mass onto the surface, 1.0 口400K thereby creating tensile stress.For films initially under 0.8 compressive stress,this effect enhances the reduction in stress in the film,as seen in Fig.2.The influence of the 0.6 surface increases as the size and energy density in cas- cades increase.An interesting point here is that such 0.4 "surface"effects can strongly influence the state of stress 0.2 in thin films,and they act on crystalline as well as amorphous films [8. 0.0t The behavior at the lowest energies clearly indicates -400 -200 0 200 400 Number of defects that radiation-induced flow commences only when the recoil energy is sufficiently high to displace an atom FIG.3.The biaxial residual stress o versus the number of from its local equilibrium site and thus create a Frenkel injected or removed atoms. 055505-2 055505-2  6 H 
0  6 H exp
YbH 6  ; (3) where   ddef=d  const. and Yb is the biaxial modulus. Here H is obtained by fitting the simulation data to Eq. (3). Typical results from the stress relaxation simulations are shown in Fig. 1 for compressive and tensile stresses. They illustrate that the stress decays exponentially with dose, that the radiation-induced vis￾cosity is independent of stress, and from the symmetry of the response to tensile and compressive stresses, that  is small. Similar behavior was observed for the other recoil energies. The principal results of the simulations are shown in Fig. 2 where the dependence of RIF is plotted as a func￾tion of recoil energy. At the lowest energies, a well￾defined threshold is observed at ET 10 eV, below which H is extremely small [ 1 10 11 Pa dpa 1, dpa: displacements per atom]. Just above this threshold, between 10 and 100 eV, the flow increases rapidly with energy. Ignoring for the moment the data above 1 keV for the simulation cells with free surfaces (open symbols), we see that above the transition regime, the flow is indepen￾dent of energy up to the highest energy examined, 10 keV. When free surfaces are available, the pressure produced within cascades induces flow of mass onto the surface, thereby creating tensile stress. For films initially under compressive stress, this effect enhances the reduction in stress in the film, as seen in Fig. 2. The influence of the surface increases as the size and energy density in cas￾cades increase. An interesting point here is that such ‘‘surface’’ effects can strongly influence the state of stress in thin films, and they act on crystalline as well as amorphous films [8]. The behavior at the lowest energies clearly indicates that radiation-induced flow commences only when the recoil energy is sufficiently high to displace an atom from its local equilibrium site and thus create a Frenkel pairlike defect. This process, therefore, very much re￾sembles the concept of ‘‘flow defects,’’ which was devel￾oped to explain thermally induced flow in amorphous alloys [13]. Within the picture that point-defect-like en￾tities mediate the radiation-induced flow, the dependence of flow on energy follows directly from the Kinchin￾Pease model of defect production, viz., no defect produc￾tion below ET, followed by a rapid increase in the number of defects just above ET, and finally a linear dependence of defects on energy above 2:5–10ET [14,15]. We have further examined this defect model of radiation-induced flow by simply injecting or removing atoms in the stressed a-CuTi matrix at randomly chosen sites and following the stress relaxation. The results of these simulations for defect creation at temperatures of 10 and 400 K are illustrated in Fig. 3, where the residual stress is plotted versus the number of added or removed atoms. The radiation-induced flow is a factor of 3 larger at the higher temperature, which is 0:7 times the glass temperature of our alloy. At 100 K (not shown) the flow is twice as large as at 10 K. Similarly, small changes in the RIF with temperature have been observed experimentally [5,8]. A surprising result observed in Fig. 3 is that the induced flow per defect is the same for injecting or removing atoms, i.e., each operates as a flow defect and -1.0 -0.5 0.0 0.5 1.0 σ0 [GPa] 0.0 0.2 0.4 0.6 0.8 1.0 1.2 H [a.u.] 0 20 40 60 80 100 -1.0 -0.5 0.0 0.5 1.0 σ/|σ0 | 500eV recoils Number of recoils FIG. 1. The RIF H is calculated from the relaxation curves for different stresses and signs of the stresses, as show in the inset. The independence of the initial stress 0 indicates Newtonian flow. 0.001 0.010 0.100 1.000 10.000 Damage energy [keV] 10-10 10-9 10-8 H [(Pa dpa)-1] with surface without surface FIG. 2. The dependence of the RIF, H, on recoil energy for simulation cells with open surface or periodic boundaries. -400 -200 0 200 400 Number of defects 0.0 0.2 0.4 0.6 0.8 1.0 1.2 σ [GPa] 10 K 400 K FIG. 3. The biaxial residual stress  versus the number of injected or removed atoms. PHYSICAL REVIEW LETTERS week ending VOLUME 90, NUMBER 5 7 FEBRUARY 2003 055505-2 055505-2