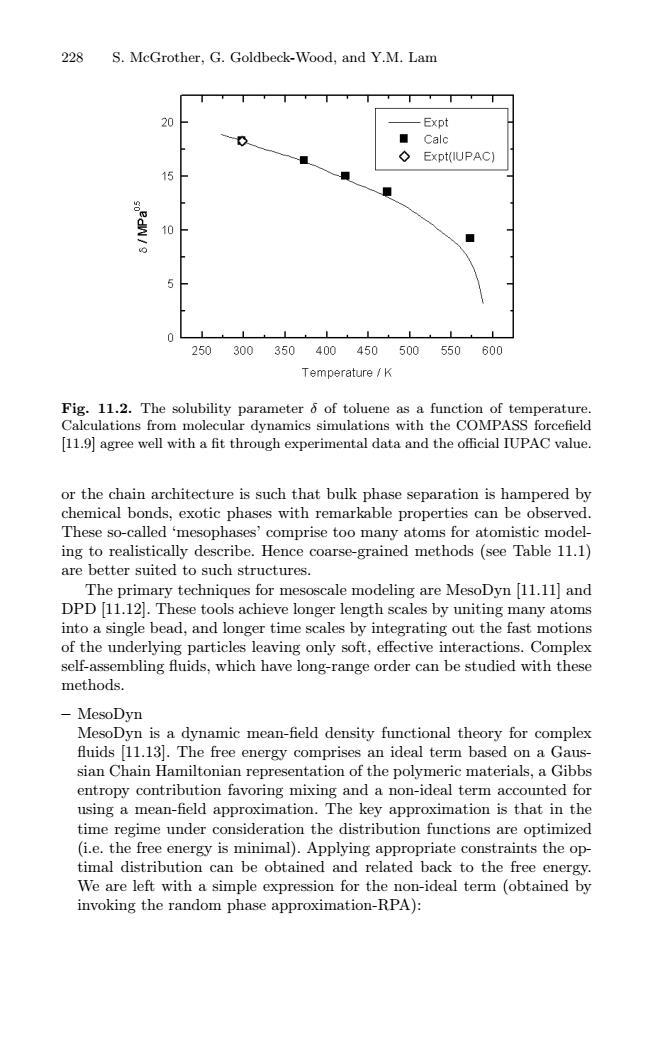
228 S.McGrother,G.Goldbeck-Wood,and Y.M.Lam 0 Expt ■ Calc 0 Expt(IUPAC】 15 LL 250300 350400450500550600 Temperature /K Fig.11.2.The solubility parameter 6 of toluene as a function of temperature. Calculations from molecular dynamics simulations with the COMPASS forcefield [11.9]agree well with a fit through experimental data and the official IUPAC value. or the chain architecture is such that bulk phase separation is hampered by chemical bonds,exotic phases with remarkable properties can be observed. These so-called 'mesophases'comprise too many atoms for atomistic model- ing to realistically describe.Hence coarse-grained methods(see Table 11.1) are better suited to such structures. The primary techniques for mesoscale modeling are MesoDyn [11.11]and DPD [11.12.These tools achieve longer length scales by uniting many atoms into a single bead,and longer time scales by integrating out the fast motions of the underlying particles leaving only soft,effective interactions.Complex self-assembling fluids,which have long-range order can be studied with these methods. MesoDyn MesoDyn is a dynamic mean-field density functional theory for complex fluids [11.13.The free energy comprises an ideal term based on a Gaus- sian Chain Hamiltonian representation of the polymeric materials,a Gibbs entropy contribution favoring mixing and a non-ideal term accounted for using a mean-field approximation.The key approximation is that in the time regime under consideration the distribution functions are optimized (i.e.the free energy is minimal).Applying appropriate constraints the op- timal distribution can be obtained and related back to the free energy. We are left with a simple expression for the non-ideal term (obtained by invoking the random phase approximation-RPA):228 S. McGrother, G. Goldbeck-Wood, and Y.M. Lam Fig. 11.2. The solubility parameter δ of toluene as a function of temperature. Calculations from molecular dynamics simulations with the COMPASS forcefield [11.9] agree well with a fit through experimental data and the official IUPAC value. or the chain architecture is such that bulk phase separation is hampered by chemical bonds, exotic phases with remarkable properties can be observed. These so-called ‘mesophases’ comprise too many atoms for atomistic model￾ing to realistically describe. Hence coarse-grained methods (see Table 11.1) are better suited to such structures. The primary techniques for mesoscale modeling are MesoDyn [11.11] and DPD [11.12]. These tools achieve longer length scales by uniting many atoms into a single bead, and longer time scales by integrating out the fast motions of the underlying particles leaving only soft, effective interactions. Complex self-assembling fluids, which have long-range order can be studied with these methods. – MesoDyn MesoDyn is a dynamic mean-field density functional theory for complex fluids [11.13]. The free energy comprises an ideal term based on a Gaus￾sian Chain Hamiltonian representation of the polymeric materials, a Gibbs entropy contribution favoring mixing and a non-ideal term accounted for using a mean-field approximation. The key approximation is that in the time regime under consideration the distribution functions are optimized (i.e. the free energy is minimal). Applying appropriate constraints the op￾timal distribution can be obtained and related back to the free energy. We are left with a simple expression for the non-ideal term (obtained by invoking the random phase approximation-RPA):