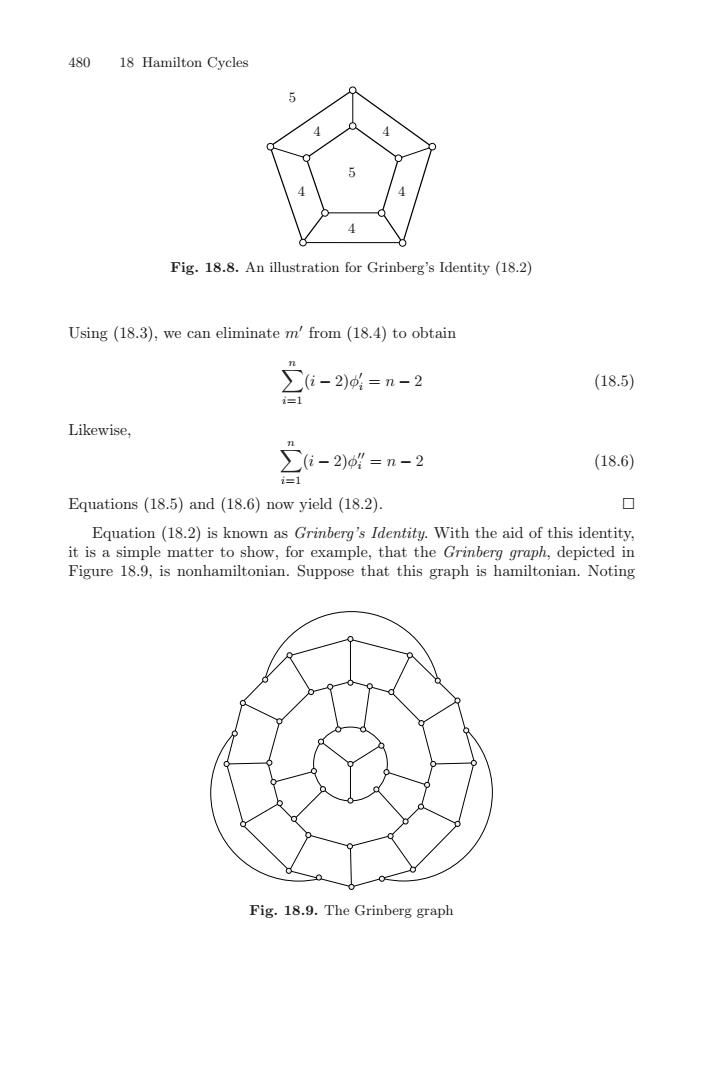
48018 Hamilton CyclesFig.18.8. An illustration for Grinberg's Identity (18.2)Using (18.3), we can eliminate m' from (18.4) to obtain(18.5)Likewise,(18.6)口Equations (18.5) and (18.6) now yield (18.2)Equation (18.2) is known as Grinberg's Identity. With the aid of this identity,itisaole mater to show,for example, that the Grinberg graph,depicted inFigure.9,isnonhamiltonian.SupposethatthisgraphishamiltonianNotingFig. 18.9. The Grinberg graph480 18 Hamilton Cycles 4 4 4 4 4 5 5 Fig. 18.8. An illustration for Grinberg’s Identity (18.2) Using (18.3), we can eliminate m from (18.4) to obtain n i=1 (i − 2)φ i = n − 2 (18.5) Likewise, n i=1 (i − 2)φ i = n − 2 (18.6) Equations (18.5) and (18.6) now yield (18.2).
Equation (18.2) is known as Grinberg’s Identity. With the aid of this identity, it is a simple matter to show, for example, that the Grinberg graph, depicted in Figure 18.9, is nonhamiltonian. Suppose that this graph is hamiltonian. Noting Fig. 18.9. The Grinberg graph