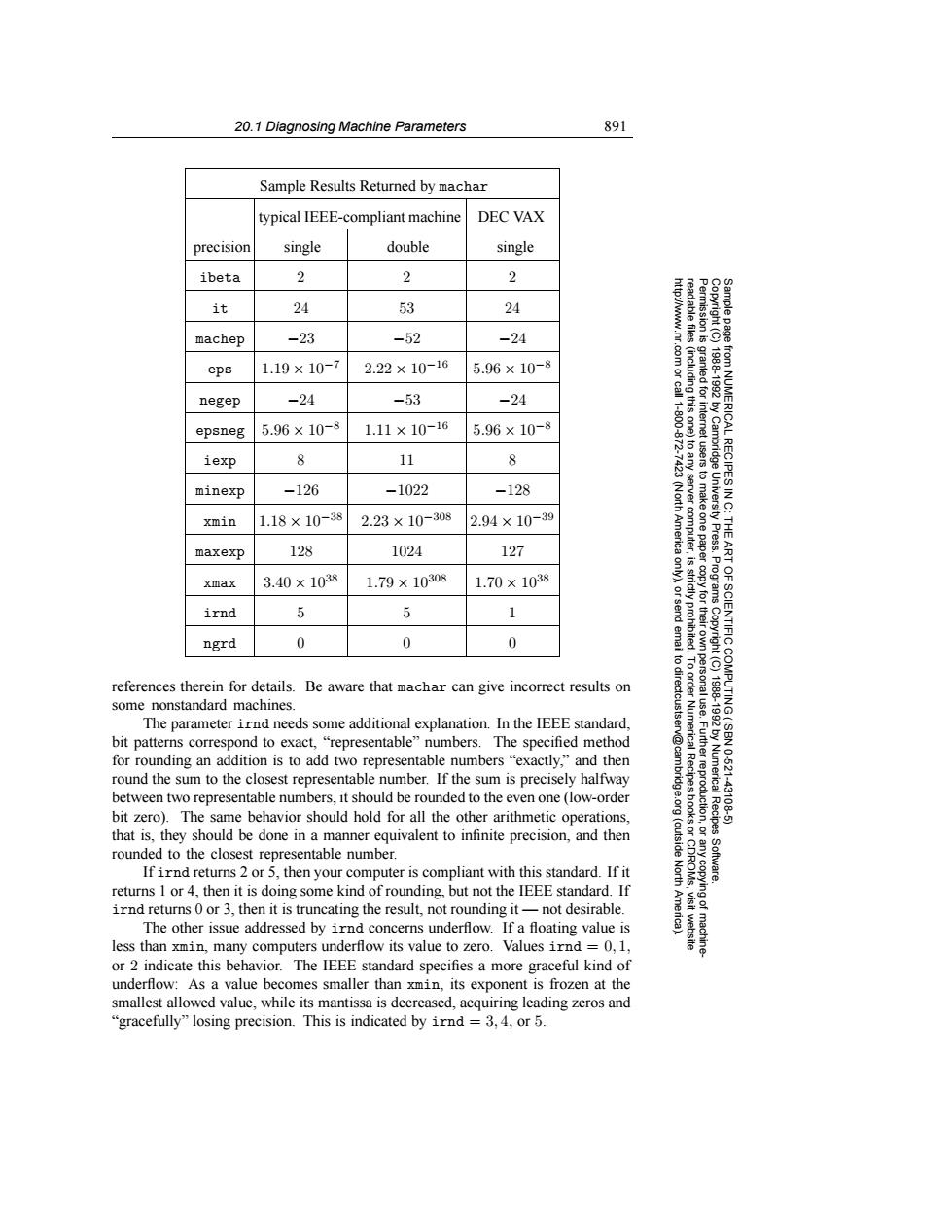
20.1 Diagnosing Machine Parameters 891 Sample Results Returned by machar typical IEEE-compliant machine DEC VAX precision single double single ibeta 2 2 2 it 24 53 24 http://www.nr. machep -23 -52 -24 eps 1.19×10-7 2.22×10-16 5.96×10-8 83 granted for negep -24 -53 -24 (including this one) 9 epsneg 5.96×10-8 1.11×10-16 5.96×10-8 111800.872 iexp 8 11 8 Cambridge minexp -126 -1022 -128 xmin 1.18×10-38 2.23×10-308 2.94×10-39 (North America to any server computer, eUniversity Press. THE maxexp 128 1024 127 ART xmax 3.40×1038 1.79×10308 1.70×1038 Programs irnd 5 5 1 send ngrd 0 0 0 to dir references therein for details.Be aware that machar can give incorrect results on some nonstandard machines. 1881892 OF SCIENTIFIC COMPUTING(ISBN The parameter irnd needs some additional explanation.In the IEEE standard, bit patterns correspond to exact,"representable"numbers.The specified method for rounding an addition is to add two representable numbers "exactly,"and then v@cam 10-521 round the sum to the closest representable number.If the sum is precisely halfway between two representable numbers,it should be rounded to the even one(low-order uurggoglrion Numerical Recipes 43108 bit zero).The same behavior should hold for all the other arithmetic operations, that is,they should be done in a manner equivalent to infinite precision,and then rounded to the closest representable number. (outside If irnd returns 2 or 5,then your computer is compliant with this standard.If it Software. returns 1 or 4,then it is doing some kind of rounding,but not the IEEE standard.If irnd returns 0 or 3,then it is truncating the result,not rounding it-not desirable. The other issue addressed by irnd concerns underflow.If a floating value is less than xmin,many computers underflow its value to zero.Values irnd =0,1, or 2 indicate this behavior.The IEEE standard specifies a more graceful kind of underflow:As a value becomes smaller than xmin,its exponent is frozen at the smallest allowed value,while its mantissa is decreased,acquiring leading zeros and "gracefully"losing precision.This is indicated by irnd =3,4,or 5.20.1 Diagnosing Machine Parameters 891 Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). Sample Results Returned by machar typical IEEE-compliant machine DEC VAX precision single double single ibeta 2 2 2 it 24 53 24 machep −23 −52 −24 eps 1.19 × 10−7 2.22 × 10−16 5.96 × 10−8 negep −24 −53 −24 epsneg 5.96 × 10−8 1.11 × 10−16 5.96 × 10−8 iexp 8 11 8 minexp −126 −1022 −128 xmin 1.18 × 10−38 2.23 × 10−308 2.94 × 10−39 maxexp 128 1024 127 xmax 3.40 × 1038 1.79 × 10308 1.70 × 1038 irnd 5 5 1 ngrd 0 0 0 references therein for details. Be aware that machar can give incorrect results on some nonstandard machines. The parameter irnd needs some additional explanation. In the IEEE standard, bit patterns correspond to exact, “representable” numbers. The specified method for rounding an addition is to add two representable numbers “exactly,” and then round the sum to the closest representable number. If the sum is precisely halfway between two representable numbers, it should be rounded to the even one (low-order bit zero). The same behavior should hold for all the other arithmetic operations, that is, they should be done in a manner equivalent to infinite precision, and then rounded to the closest representable number. If irnd returns 2 or 5, then your computer is compliant with this standard. If it returns 1 or 4, then it is doing some kind of rounding, but not the IEEE standard. If irnd returns 0 or 3, then it is truncating the result, not rounding it — not desirable. The other issue addressed by irnd concerns underflow. If a floating value is less than xmin, many computers underflow its value to zero. Values irnd = 0, 1, or 2 indicate this behavior. The IEEE standard specifies a more graceful kind of underflow: As a value becomes smaller than xmin, its exponent is frozen at the smallest allowed value, while its mantissa is decreased, acquiring leading zeros and “gracefully” losing precision. This is indicated by irnd = 3, 4, or 5