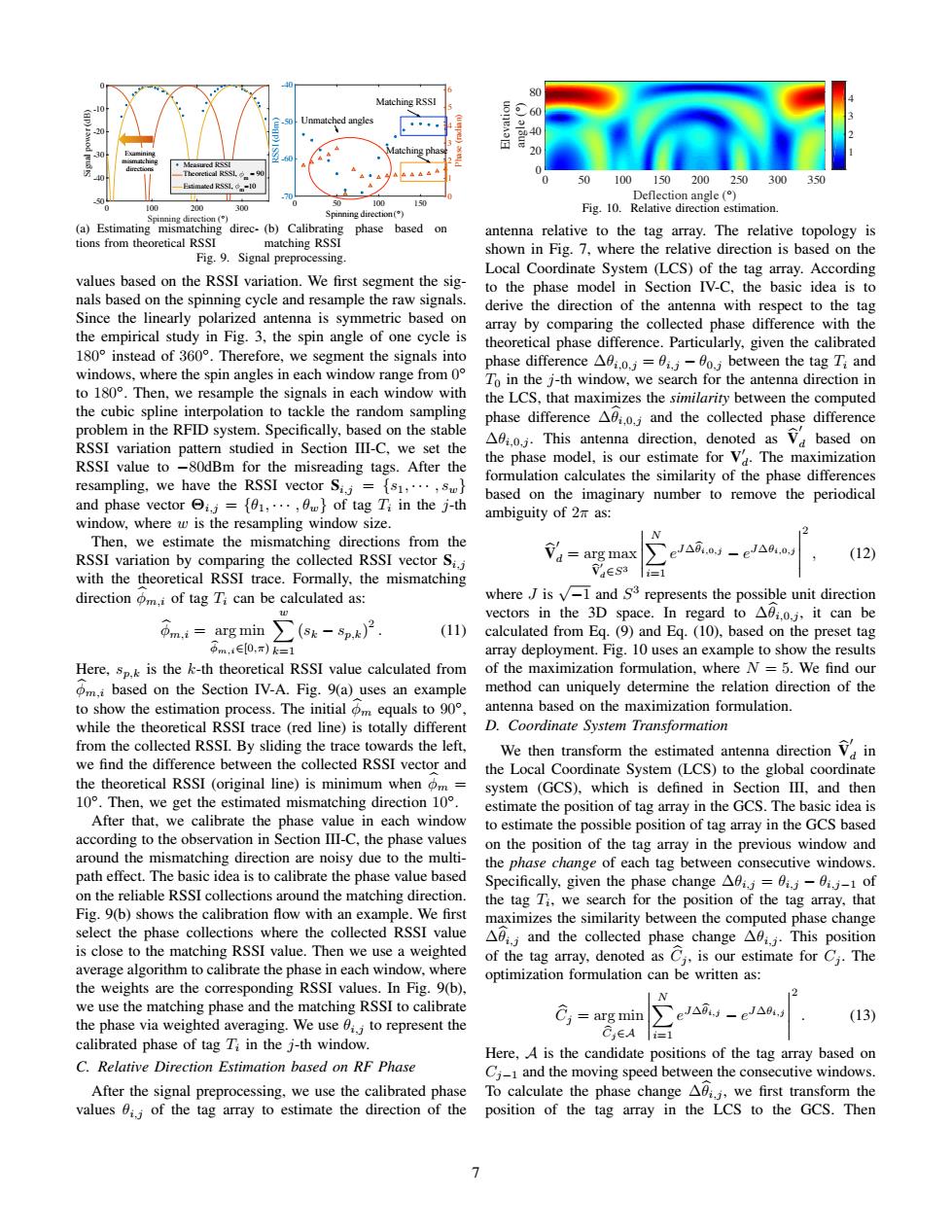
80 Matching RSSI 60 Unmatched angles (3]3ue 24 ed Rss 50 Estimaed RSSI. 100150200250300 Deflection angle() 00 200 Fig.10.Relative direction estimation. direc-(b)Calibrating phase based on antenna relative to the tag array.The relative topology is tions from theoretical RSSI matching RSSI shown in Fig.7,where the relative direction is based on the Fig.9.Signal preprocessing Local Coordinate System (LCS)of the tag array.According values based on the RSSI variation.We first segment the sig- to the phase model in Section IV-C.,the basic idea is to nals based on the spinning cycle and resample the raw signals. derive the direction of the antenna with respect to the tag Since the linearly polarized antenna is symmetric based on array by comparing the collected phase difference with the the empirical study in Fig.3,the spin angle of one cycle is theoretical phase difference.Particularly,given the calibrated 180 instead of 360.Therefore,we segment the signals into phase difference A0i.0.j=0:.j-00.;between the tag Ti and windows,where the spin angles in each window range from 0 To in the j-th window,we search for the antenna direction in to 180.Then,we resample the signals in each window with the LCS,that maximizes the similarity between the computed the cubic spline interpolation to tackle the random sampling phase difference A.0.and the collected phase difference problem in the RFID system.Specifically,based on the stable RSSI variation pattern studied in Section III-C,we set the Ao.This antenna direction,denoted as based on RSSI value to -80dBm for the misreading tags.After the the phase model,is our estimate for V.The maximization resampling,we have the RSSI vector Si={s1,...,s} formulation calculates the similarity of the phase differences based on the imaginary number to remove the periodical and phase vector i.=01,...,}of tag Ti in the j-th ambiguity of2πas: window,where w is the resampling window size. Then,we estimate the mismatching directions from the RSSI variation by comparing the collected RSSI vector Sij 寸a=arg max J△.0d-eJ△84,0J (12) with the theoretical RSSI trace.Formally,the mismatching Vaesa direction m.i of tag Ti can be calculated as: whereJ is v-I and S3 represents the possible unit direction vectors in the 3D space.In regard to A0i.0.j,it can be om.=arg min (sk -sp)2. (11) calculated from Eq.(9)and Eq.(10),based on the preset tag pm,∈0，x）k=1 array deployment.Fig.10 uses an example to show the results Here,sp.is the k-th theoretical RSSI value calculated from of the maximization formulation,where N=5.We find our m.i based on the Section IV-A.Fig.9(a)uses an example method can uniquely determine the relation direction of the to show the estimation process.The initial m equals to 90, antenna based on the maximization formulation. while the theoretical RSSI trace (red line)is totally different D.Coordinate System Transformation from the collected RSSI.By sliding the trace towards the left, We then transform the estimated antenna directionV in we find the difference between the collected RSSI vector and the Local Coordinate System (LCS)to the global coordinate the theoretical RSSI (original line)is minimum when om= system (GCS),which is defined in Section III,and then 10.Then,we get the estimated mismatching direction 10. estimate the position of tag array in the GCS.The basic idea is After that,we calibrate the phase value in each window to estimate the possible position of tag array in the GCS based according to the observation in Section III-C,the phase values on the position of the tag array in the previous window and around the mismatching direction are noisy due to the multi- the phase change of each tag between consecutive windows. path effect.The basic idea is to calibrate the phase value based Specifically,given the phase change A0ij=0.j-0j-1 of on the reliable RSSI collections around the matching direction. the tag Ti,we search for the position of the tag array,that Fig.9(b)shows the calibration flow with an example.We first maximizes the similarity between the computed phase change select the phase collections where the collected RSSI value Aij and the collected phase change Aij.This position is close to the matching RSSI value.Then we use a weighted of the tag array,denoted as C.is our estimate for Cj The average algorithm to calibrate the phase in each window.where optimization formulation can be written as: the weights are the corresponding RSSI values.In Fig.9(b), we use the matching phase and the matching RSSI to calibrate the phase via weighted averaging.We use ii to represent the C=arg min J△i-eJ△8， (13) CEA calibrated phase of tag T in the j-th window. Here,A is the candidate positions of the tag array based on C.Relative Direction Estimation based on RF Phase C-1 and the moving speed between the consecutive windows. After the signal preprocessing,we use the calibrated phase To calculate the phase change Aj,we first transform the values 6i;of the tag array to estimate the direction of the position of the tag array in the LCS to the GCS.Then >0 100 200 300 Spinning direction (°) -50 -40 -30 -20 -10 0 Signal power (dB) Measured RSSI Theoretical RSSI, m = 90 Estimated RSSI, m=10 Examining mismatching directions (a) Estimating mismatching direc￾tions from theoretical RSSI 0 50 100 150 Spinning angle (°) -70 -60 -50 -40 RSSI (dBm) 0 1 2 3 4 5 6 Phase (radian) Matching RSSI Matching phase Unmatched angles Spinning direction (b) Calibrating phase based on matching RSSI Fig. 9. Signal preprocessing. values based on the RSSI variation. We first segment the sig￾nals based on the spinning cycle and resample the raw signals. Since the linearly polarized antenna is symmetric based on the empirical study in Fig. 3, the spin angle of one cycle is 180◦ instead of 360◦ . Therefore, we segment the signals into windows, where the spin angles in each window range from 0 ◦ to 180◦ . Then, we resample the signals in each window with the cubic spline interpolation to tackle the random sampling problem in the RFID system. Specifically, based on the stable RSSI variation pattern studied in Section III-C, we set the RSSI value to −80dBm for the misreading tags. After the resampling, we have the RSSI vector Si,j = {s1, · · · , sw} and phase vector Θi,j = {θ1, · · · , θw} of tag Ti in the j-th window, where w is the resampling window size. Then, we estimate the mismatching directions from the RSSI variation by comparing the collected RSSI vector Si,j with the theoretical RSSI trace. Formally, the mismatching direction φbm,i of tag Ti can be calculated as: φbm,i = arg min φbm,i∈[0,π) Xw k=1 (sk − sp,k) 2 . (11) Here, sp,k is the k-th theoretical RSSI value calculated from φbm,i based on the Section IV-A. Fig. 9(a) uses an example to show the estimation process. The initial φbm equals to 90◦ , while the theoretical RSSI trace (red line) is totally different from the collected RSSI. By sliding the trace towards the left, we find the difference between the collected RSSI vector and the theoretical RSSI (original line) is minimum when φbm = 10◦ . Then, we get the estimated mismatching direction 10◦ . After that, we calibrate the phase value in each window according to the observation in Section III-C, the phase values around the mismatching direction are noisy due to the multi￾path effect. The basic idea is to calibrate the phase value based on the reliable RSSI collections around the matching direction. Fig. 9(b) shows the calibration flow with an example. We first select the phase collections where the collected RSSI value is close to the matching RSSI value. Then we use a weighted average algorithm to calibrate the phase in each window, where the weights are the corresponding RSSI values. In Fig. 9(b), we use the matching phase and the matching RSSI to calibrate the phase via weighted averaging. We use θi,j to represent the calibrated phase of tag Ti in the j-th window. C. Relative Direction Estimation based on RF Phase After the signal preprocessing, we use the calibrated phase values θi,j of the tag array to estimate the direction of the 0 50 100 150 200 250 300 350 Deflection angle (°) 0 20 40 60 80 Elevation angle ( ° ) 1 2 3 4 Fig. 10. Relative direction estimation. antenna relative to the tag array. The relative topology is shown in Fig. 7, where the relative direction is based on the Local Coordinate System (LCS) of the tag array. According to the phase model in Section IV-C, the basic idea is to derive the direction of the antenna with respect to the tag array by comparing the collected phase difference with the theoretical phase difference. Particularly, given the calibrated phase difference ∆θi,0,j = θi,j − θ0,j between the tag Ti and T0 in the j-th window, we search for the antenna direction in the LCS, that maximizes the similarity between the computed phase difference ∆θbi,0,j and the collected phase difference ∆θi,0,j . This antenna direction, denoted as Vb 0 d based on the phase model, is our estimate for V 0 d . The maximization formulation calculates the similarity of the phase differences based on the imaginary number to remove the periodical ambiguity of 2π as: Vb 0 d = arg max Vb 0 d∈S3      X N i=1 e J∆θbi,0,j − e J∆θi,0,j      2 , (12) where J is √ −1 and S 3 represents the possible unit direction vectors in the 3D space. In regard to ∆θbi,0,j , it can be calculated from Eq. (9) and Eq. (10), based on the preset tag array deployment. Fig. 10 uses an example to show the results of the maximization formulation, where N = 5. We find our method can uniquely determine the relation direction of the antenna based on the maximization formulation. D. Coordinate System Transformation We then transform the estimated antenna direction Vb 0 d in the Local Coordinate System (LCS) to the global coordinate system (GCS), which is defined in Section III, and then estimate the position of tag array in the GCS. The basic idea is to estimate the possible position of tag array in the GCS based on the position of the tag array in the previous window and the phase change of each tag between consecutive windows. Specifically, given the phase change ∆θi,j = θi,j − θi,j−1 of the tag Ti , we search for the position of the tag array, that maximizes the similarity between the computed phase change ∆θbi,j and the collected phase change ∆θi,j . This position of the tag array, denoted as Cbj , is our estimate for Cj . The optimization formulation can be written as: Cbj = arg min Cbj∈A      X N i=1 e J∆θbi,j − e J∆θi,j      2 . (13) Here, A is the candidate positions of the tag array based on Cj−1 and the moving speed between the consecutive windows. To calculate the phase change ∆θbi,j , we first transform the position of the tag array in the LCS to the GCS. Then 7