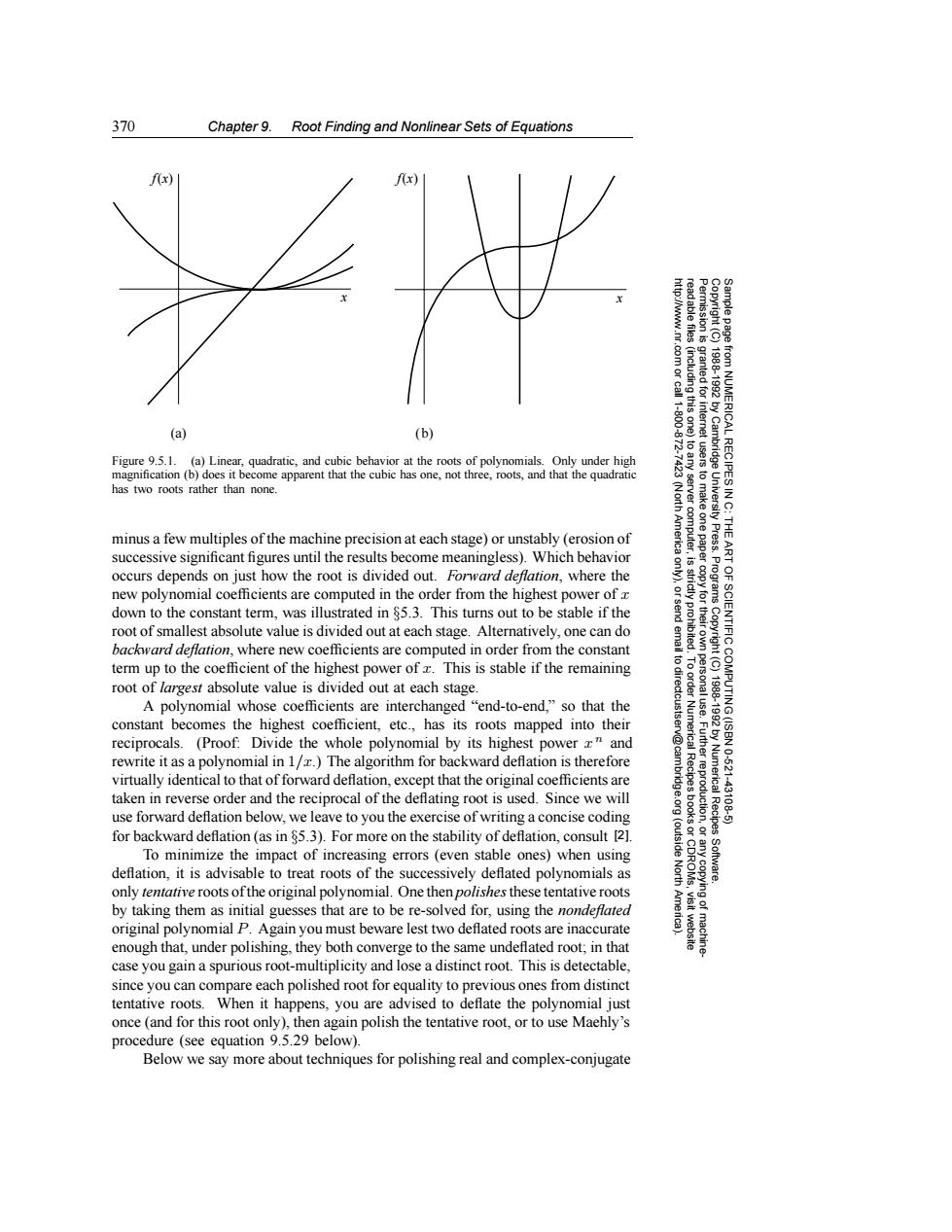
370 Chapter 9.Root Finding and Nonlinear Sets of Equations fx) 八x) e小N 83 from NUMERICAL RECIPESI 188891992 11800 (a) (b) Figure 9.5.1.(a)Linear,quadratic,and cubic behavior at the roots of polynomials.Only under high magnification (b)does it become apparent that the cubic has one,not three,roots,and that the quadratic has two roots rather than none. 9 minus a few multiples of the machine precision at each stage)or unstably (erosion of America computer, successive significant figures until the results become meaningless).Which behavior 9。 occurs depends on just how the root is divided out.Forward deflation,where the new polynomial coefficients are computed in the order from the highest power of x 9 down to the constant term,was illustrated in $5.3.This turns out to be stable if the root of smallest absolute value is divided out at each stage.Alternatively.one can do backward deflation,where new coefficients are computed in order from the constant term up to the coefficient of the highest power of z.This is stable if the remaining 可 root of largest absolute value is divided out at each stage. A polynomial whose coefficients are interchanged "end-to-end,"so that the constant becomes the highest coefficient,etc.,has its roots mapped into their reciprocals.(Proof:Divide the whole polynomial by its highest power x and rewrite it as a polynomial in 1/z.)The algorithm for backward deflation is therefore Fuurggoglrion Numerical Recipes 10621 virtually identical to that of forward deflation,except that the original coefficients are taken in reverse order and the reciprocal of the deflating root is used.Since we will 43108 use forward deflation below,we leave to you the exercise of writing a concise coding for backward deflation (as in 85.3).For more on the stability of deflation.consult [2]. To minimize the impact of increasing errors(even stable ones)when using (outside deflation.it is advisable to treat roots of the successively deflated polynomials as North Software. only tentative roots ofthe original polynomial.One then polishes these tentative roots by taking them as initial guesses that are to be re-solved for,using the nondeflated original polynomial P.Again you must beware lest two deflated roots are inaccurate enough that,under polishing,they both converge to the same undeflated root;in that case you gain a spurious root-multiplicity and lose a distinct root.This is detectable. since you can compare each polished root for equality to previous ones from distinct tentative roots.When it happens,you are advised to deflate the polynomial just once (and for this root only),then again polish the tentative root,or to use Maehly's procedure (see equation 9.5.29 below). Below we say more about techniques for polishing real and complex-conjugate370 Chapter 9. Root Finding and Nonlinear Sets of Equations Permission is granted for internet users to make one paper copy for their own personal use. Further reproduction, or any copyin Copyright (C) 1988-1992 by Cambridge University Press. Programs Copyright (C) 1988-1992 by Numerical Recipes Software. Sample page from NUMERICAL RECIPES IN C: THE ART OF SCIENTIFIC COMPUTING (ISBN 0-521-43108-5) g of machine￾readable files (including this one) to any server computer, is strictly prohibited. To order Numerical Recipes books or CDROMs, visit website http://www.nr.com or call 1-800-872-7423 (North America only), or send email to directcustserv@cambridge.org (outside North America). (a) x x (b) f(x) f(x) Figure 9.5.1. (a) Linear, quadratic, and cubic behavior at the roots of polynomials. Only under high magnification (b) does it become apparent that the cubic has one, not three, roots, and that the quadratic has two roots rather than none. minus a few multiples of the machine precision at each stage) or unstably (erosion of successive significant figures until the results become meaningless). Which behavior occurs depends on just how the root is divided out. Forward deflation, where the new polynomial coefficients are computed in the order from the highest power of x down to the constant term, was illustrated in §5.3. This turns out to be stable if the root of smallest absolute value is divided out at each stage. Alternatively, one can do backward deflation, where new coefficients are computed in order from the constant term up to the coefficient of the highest power of x. This is stable if the remaining root of largest absolute value is divided out at each stage. A polynomial whose coefficients are interchanged “end-to-end,” so that the constant becomes the highest coefficient, etc., has its roots mapped into their reciprocals. (Proof: Divide the whole polynomial by its highest power x n and rewrite it as a polynomial in 1/x.) The algorithm for backward deflation is therefore virtually identical to that of forward deflation, except that the original coefficients are taken in reverse order and the reciprocal of the deflating root is used. Since we will use forward deflation below, we leave to you the exercise of writing a concise coding for backward deflation (as in §5.3). For more on the stability of deflation, consult [2]. To minimize the impact of increasing errors (even stable ones) when using deflation, it is advisable to treat roots of the successively deflated polynomials as only tentative roots of the original polynomial. One then polishesthese tentative roots by taking them as initial guesses that are to be re-solved for, using the nondeflated original polynomial P. Again you must beware lest two deflated roots are inaccurate enough that, under polishing, they both converge to the same undeflated root; in that case you gain a spurious root-multiplicity and lose a distinct root. This is detectable, since you can compare each polished root for equality to previous ones from distinct tentative roots. When it happens, you are advised to deflate the polynomial just once (and for this root only), then again polish the tentative root, or to use Maehly’s procedure (see equation 9.5.29 below). Below we say more about techniques for polishing real and complex-conjugate