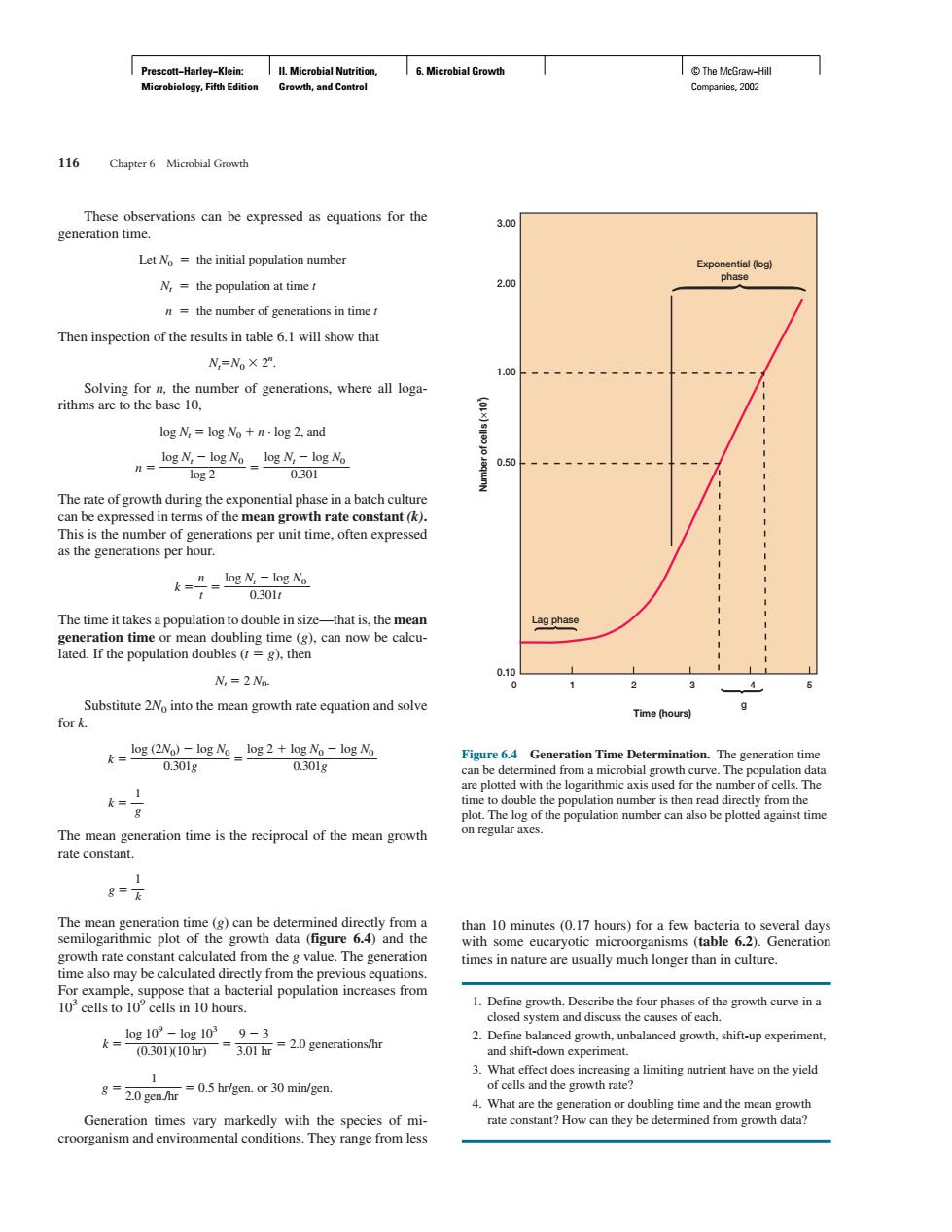
6.Microbial Growth 6 Chapter 6 Microbial Growth These observations can be equations for the Let No=the initial population number Nthe population at time ho) n=the number of generations in time t Then inspection of the results in table 6.1 will show that N=×2” Solving for n,the number of generations.where all loga rithms are to the base 10. log N,=log No+nlog 2.and -s水-s The time it takes a populatic to double in size thatis the m N=2No Time (hours) k-s2g4.s2+g-s Figu re 6.4 Gen tion Time Determination.The tion tim ve.I re plotted wi h the of c The mean generation time is the reciprocal of the mean growth rate constant The mean generation time ()can be determined directly from semilogarithmic plot of the growth data (figure 6.4)and the times in nature are usually much longer than in culture. 2.Defne ubalanced gwthif-uxrmt alimiting utrient have on the yield 20 gen/r0.5 hr/gen.or 30 min/gen Generation times vary markedly with the species of mi croorganism and environmental conditions.They range from lessPrescott−Harley−Klein: Microbiology, Fifth Edition II. Microbial Nutrition, Growth, and Control 6. Microbial Growth © The McGraw−Hill Companies, 2002 These observations can be expressed as equations for the generation time. Let N0 the initial population number Nt the population at time t n the number of generations in time t Then inspection of the results in table 6.1 will show that Nt N0
2n . Solving for n, the number of generations, where all loga￾rithms are to the base 10, log Nt log N0 n · log 2, and log Nt  log N0 log Nt  log N0 n ______________ ______________ log 2 0.301 The rate of growth during the exponential phase in a batch culture can be expressed in terms of the mean growth rate constant (k). This is the number of generations per unit time, often expressed as the generations per hour. n log Nt  log N0 k __ ______________ t 0.301t The time it takes a population to double in size—that is, the mean generation time or mean doubling time (g), can now be calcu￾lated. If the population doubles (t g), then Nt 2 N0. Substitute 2N0 into the mean growth rate equation and solve for k. log (2N0)  log N0 log 2 log N0  log N0 k ________________ _____________________ 0.301g 0.301g 1 k __ g The mean generation time is the reciprocal of the mean growth rate constant. 1 g __ k The mean generation time (g) can be determined directly from a semilogarithmic plot of the growth data (figure 6.4) and the growth rate constant calculated from the g value. The generation time also may be calculated directly from the previous equations. For example, suppose that a bacterial population increases from 103 cells to 109 cells in 10 hours. log 109  log 103 9  3 k _______________ ______ 2.0 generations/hr (0.301)(10 hr) 3.01 hr 1 g _________ 0.5 hr/gen. or 30 min/gen. 2.0 gen./hr Generation times vary markedly with the species of mi￾croorganism and environmental conditions. They range from less than 10 minutes (0.17 hours) for a few bacteria to several days with some eucaryotic microorganisms (table 6.2). Generation times in nature are usually much longer than in culture. 1. Define growth. Describe the four phases of the growth curve in a closed system and discuss the causes of each. 2. Define balanced growth, unbalanced growth, shift-up experiment, and shift-down experiment. 3. What effect does increasing a limiting nutrient have on the yield of cells and the growth rate? 4. What are the generation or doubling time and the mean growth rate constant? How can they be determined from growth data? 116 Chapter 6 Microbial Growth Time (hours) Number of cells (×107 ) 1 2 3 45 g 0 0.10 0.50 1.00 2.00 3.00 Lag phase Exponential (log) phase Figure 6.4 Generation Time Determination. The generation time can be determined from a microbial growth curve. The population data are plotted with the logarithmic axis used for the number of cells. The time to double the population number is then read directly from the plot. The log of the population number can also be plotted against time on regular axes.