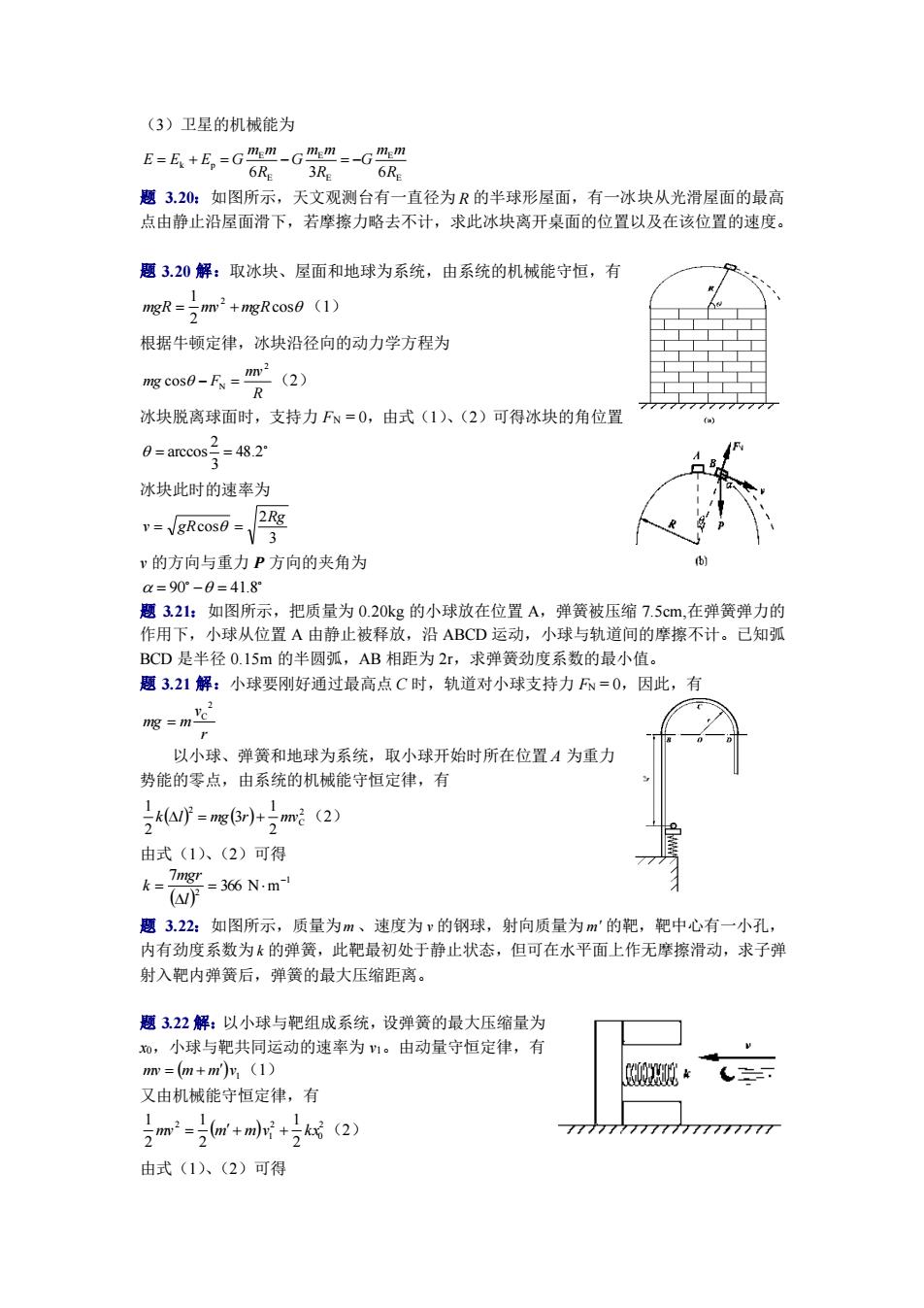
(3)卫星的机板能为 E-B+5-G8m-G5。-G%m 6R说6R 题3确如图所示，天文观测台有一直径为R的半球形屋面。有一冰块从光滑屋面的最高 点由静止沿屋面滑下，若摩擦力略去不计，求北冰块离开桌面的位置以及在该位置的速度。 题3,20解：取冰块、隧面和地球为系统，由系统的机械能守恒。有 Rmco0 (1) 根据牛顿定律，冰块沿径向的动力学方程为 mg cos0-F=m (2 冰块脱离球面时，支持力F⅓=0，由式《1)、(2)可得冰块的角位置 0-c0s2 482 冰块此时的速率为 -am0-浮 ￥的方白与重力P方向的夹角为 a=90-0=418 思321：如图所示，把质量为020味g的小球故在位置A,弹簧被压缩7.5m,在弹簧弹力的 作用下，小球从位置A由静止被释放，沿A政CD运动。小球与轨道间的摩擦不计，己知弧 BCD是半径0.15m的半圆弧，AB相距为2：，求弹簧劲度系量的最小值。 题3.21解，小球要刚好通过最高点C时，轨道对小球支持力=0，因此，有 =m& 以小球，弹簧和地球为系饶，取小缘开始时所在位置A为重力 势能的零点，由系统的机械能守恒定律，有 af-嗯6r+2E2) 由式(1)、(2)可得 7me3 N.m W 题322如图所示，质量为m、速度为的钢球，射向质量为m的靶，无中心有一小孔， 内有劲度系数为，的弹簧，此视最初处于静止状态，但可在水平面上作无摩擦滑动。求子弹 射入无内弹簧后，弹簧的最大压缩距离。 题122解：以小球与视组成系统，设弹蔬的最大压缩量为 静，小球与肥共同运动的速率为的。由动量守恒定律，有 m=m+无(I) 又由机械能守恒定律。有 w2-r+m城+城a 777717777777777777 由式《1)、(2)可得（3）卫星的机械能为 E E E E E E k p 6 3 6R m m G R m m G R m m E = E + E = G − = − 题 3.20：如图所示，天文观测台有一直径为 R 的半球形屋面，有一冰块从光滑屋面的最高 点由静止沿屋面滑下，若摩擦力略去不计，求此冰块离开桌面的位置以及在该位置的速度。 题 3.20 解：取冰块、屋面和地球为系统，由系统的机械能守恒，有 cos 2 1 2 mgR = mv + mgR （1） 根据牛顿定律，冰块沿径向的动力学方程为 R mv mg F 2 N cos − = （2） 冰块脱离球面时，支持力 FN = 0，由式（1）、（2）可得冰块的角位置  48.2 3 2  = arccos = 冰块此时的速率为 3 2 cos Rg v = gR  = v 的方向与重力 P 方向的夹角为    = 90 − = 41.8 题 3.21：如图所示，把质量为 0.20kg 的小球放在位置 A，弹簧被压缩 7.5cm,在弹簧弹力的 作用下，小球从位置 A 由静止被释放，沿 ABCD 运动，小球与轨道间的摩擦不计。已知弧 BCD 是半径 0.15m 的半圆弧，AB 相距为 2r，求弹簧劲度系数的最小值。 题 3.21 解：小球要刚好通过最高点 C 时，轨道对小球支持力 FN = 0，因此，有 r v mg m 2 C = 以小球、弹簧和地球为系统，取小球开始时所在位置 A 为重力 势能的零点，由系统的机械能守恒定律，有 ( ) ( ) 2 C 2 2 1 3 2 1 k l = mg r + mv （2） 由式（1）、（2）可得 ( ) 1 2 366 N m 7 − =   = l mgr k 题 3.22：如图所示，质量为 m 、速度为 v 的钢球，射向质量为 m  的靶，靶中心有一小孔， 内有劲度系数为 k 的弹簧，此靶最初处于静止状态，但可在水平面上作无摩擦滑动，求子弹 射入靶内弹簧后，弹簧的最大压缩距离。 题 3.22 解：以小球与靶组成系统，设弹簧的最大压缩量为 x0，小球与靶共同运动的速率为 v1。由动量守恒定律，有 ( ) 1 mv = m + m  v （1） 又由机械能守恒定律，有 ( ) 2 0 2 1 2 2 1 2 1 2 1 mv = m  + m v + kx （2） 由式（1）、（2）可得