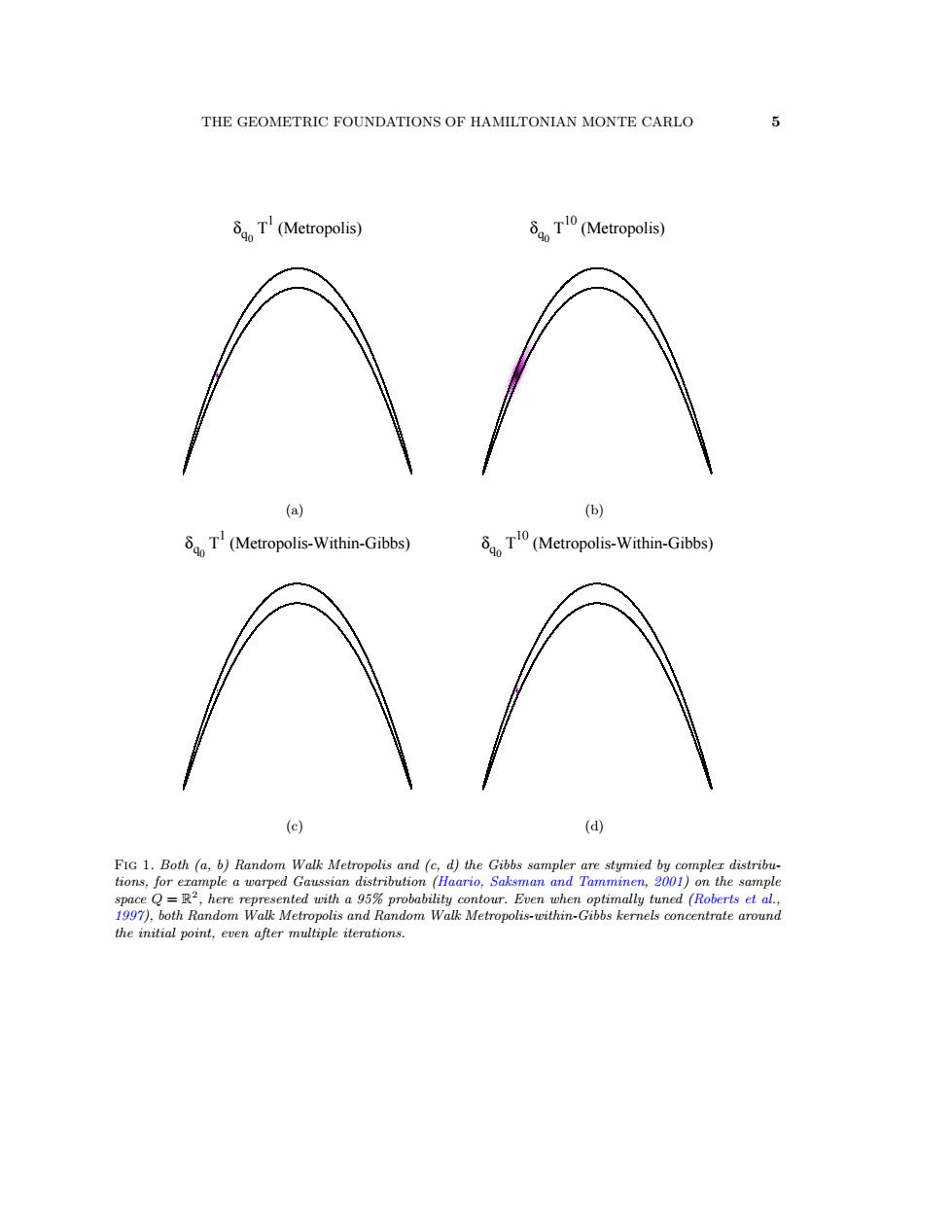
THE GEOMETRIC FOUNDATIONS OF HAMILTONIAN MONTE CARLO T(Metropolis) δa,T(Metropolis) T(Metropolis-Within-Gibbs) I (Metropolis-Within-Gibbs (c) (d) the initial point,een aftermultiple iterntions. THE GEOMETRIC FOUNDATIONS OF HAMILTONIAN MONTE CARLO 5 δq0 T1 (Metropolis) (a) δq0 T10 (Metropolis) (b) δq0 T1 (Metropolis-Within-Gibbs) (c) δq0 T10 (Metropolis-Within-Gibbs) (d) Fig 1. Both (a, b) Random Walk Metropolis and (c, d) the Gibbs sampler are stymied by complex distribu￾tions, for example a warped Gaussian distribution (Haario, Saksman and Tamminen, 2001) on the sample space Q = R 2 , here represented with a 95% probability contour. Even when optimally tuned (Roberts et al., 1997), both Random Walk Metropolis and Random Walk Metropolis-within-Gibbs kernels concentrate around the initial point, even after multiple iterations