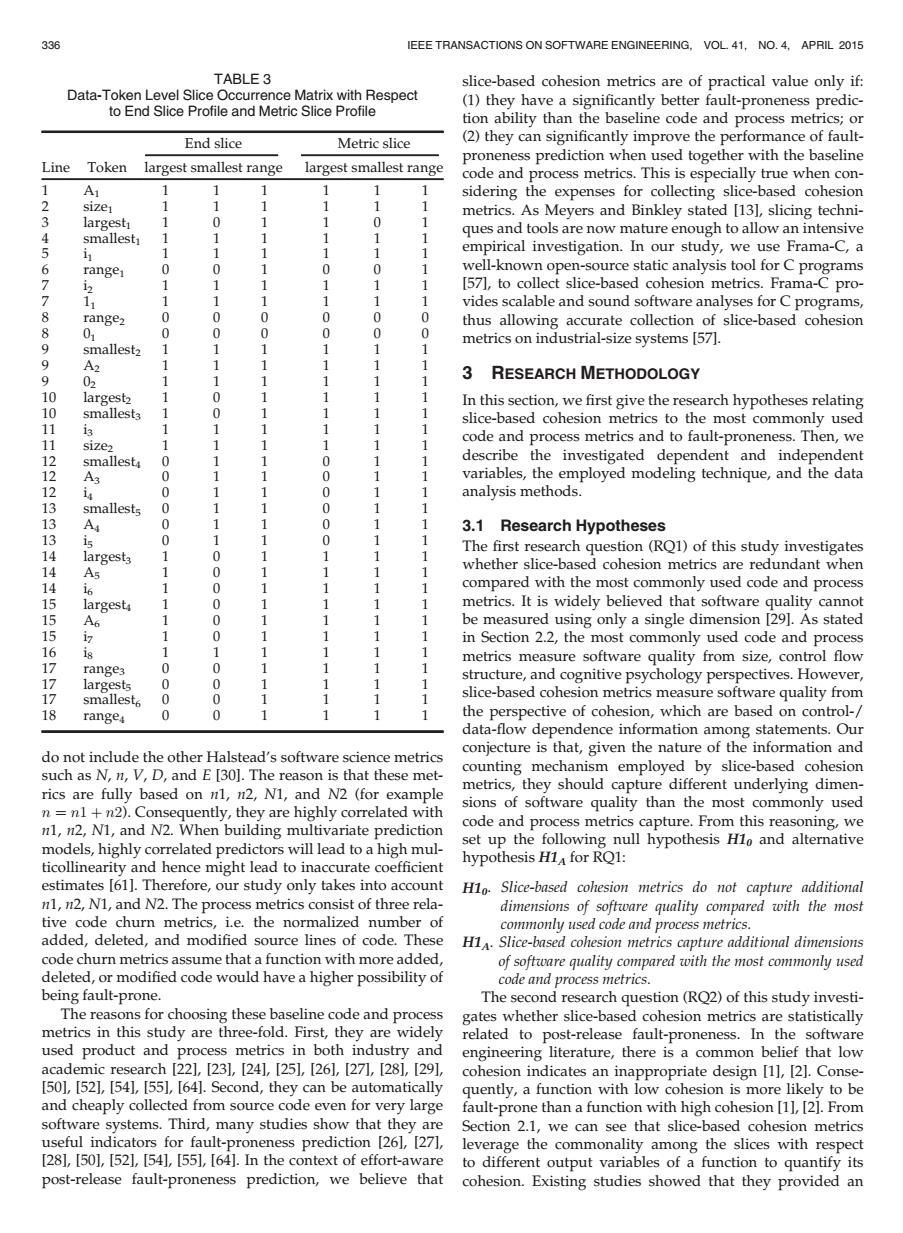
336 IEEE TRANSACTIONS ON SOFTWARE ENGINEERING,VOL 41,NO.4,APRIL 2015 TABLE 3 slice-based cohesion metrics are of practical value only if: Data-Token Level Slice Occurrence Matrix with Respect (1)they have a significantly better fault-proneness predic- to End Slice Profile and Metric Slice Profile tion ability than the baseline code and process metrics;or End slice Metric slice (2)they can significantly improve the performance of fault- proneness prediction when used together with the baseline Line Token largest smallest range largest smallest range code and process metrics.This is especially true when con- A1 sidering the expenses for collecting slice-based cohesion size1 metrics.As Meyers and Binkley stated [13],slicing techni- 3 largesti 0 smallest ques and tools are now mature enough to allow an intensive 4 5 empirical investigation.In our study,we use Frama-C,a 6 range 0 0 well-known open-source static analysis tool for C programs 7 1 [57],to collect slice-based cohesion metrics.Frama-C pro- 7 vides scalable and sound software analyses for C programs, 8 range? 0 0 0 0 thus allowing accurate collection of slice-based cohesion 8 01 0 0 0 0 metrics on industrial-size systems [57]. 9 smallest2 9 A2 3 RESEARCH METHODOLOGY 02 10 largest2 In this section,we first give the research hypotheses relating 10 smallesta slice-based cohesion metrics to the most commonly used 11 i3 11 code and process metrics and to fault-proneness.Then,we size2 12 smallest 0 describe the investigated dependent and independent 12 A3 0 0 variables,the employed modeling technique,and the data 0 0 analysis methods 3 smallests 0 0 0 1 0 3.1 Research Hypotheses 13 0 人 0 The first research question(RQ1)of this study investigates 14 whether slice-based cohesion metrics are redundant when 14 16 compared with the most commonly used code and process 15 largest4 metrics.It is widely believed that software quality cannot 1 A6 0 be measured using only a single dimension [291.As stated 15 0 in Section 2.2,the most commonly used code and process 16 is metrics measure software quality from size,control flow 17 range3 0 0 largests 0 0 structure,and cognitive psychology perspectives.However, 17 smallest 0 0 slice-based cohesion metrics measure software quality from 18 range 0 0 the perspective of cohesion,which are based on control-/ data-flow dependence information among statements.Our do not include the other Halstead's software science metrics conjecture is that,given the nature of the information and such as N,n,V,D,and E [30].The reason is that these met- counting mechanism employed by slice-based cohesion rics are fully based on n1,n2,N1,and N2 (for example metrics,they should capture different underlying dimen- sions of software quality than the most commonly used n=n1 +n2).Consequently,they are highly correlated with n1,n2,N1,and N2.When building multivariate prediction code and process metrics capture.From this reasoning,we models,highly correlated predictors will lead to a high mul- set up the following null hypothesis Hlo and alternative ticollinearity and hence might lead to inaccurate coefficient hypothesis HI for RQ1: estimates [61].Therefore,our study only takes into account H1o.Slice-based cohesion metrics do not capture additional n1,n2,N1,and N2.The process metrics consist of three rela- dimensions of software quality compared with the most tive code churn metrics,i.e.the normalized number of commonly used code and process metrics. added,deleted,and modified source lines of code.These H1A.Slice-based cohesion metrics capture additional dimensions code churn metrics assume that a function with more added, of software quality compared with the most commonly used deleted,or modified code would have a higher possibility of code and process metrics. being fault-prone. The second research question (RO2)of this study investi- The reasons for choosing these baseline code and process gates whether slice-based cohesion metrics are statistically metrics in this study are three-fold.First,they are widely related to post-release fault-proneness.In the software used product and process metrics in both industry and engineering literature,there is a common belief that low academic research[22],[23l,[241,[25],[26l,[27,[28l,[29], cohesion indicates an inappropriate design [1],[2].Conse- [50],[52],[54],[55],[64].Second,they can be automatically quently,a function with low cohesion is more likely to be and cheaply collected from source code even for very large fault-prone than a function with high cohesion [1],[2].From software systems.Third,many studies show that they are Section 2.1,we can see that slice-based cohesion metrics useful indicators for fault-proneness prediction [261,[27], leverage the commonality among the slices with respect [281,[501,[521,[54],551,[64].In the context of effort-aware to different output variables of a function to quantify its post-release fault-proneness prediction,we believe that cohesion.Existing studies showed that they provided ando not include the other Halstead’s software science metrics such as N, n, V, D, and E [30]. The reason is that these met￾rics are fully based on n1, n2, N1, and N2 (for example n ¼ n1 þ n2). Consequently, they are highly correlated with n1, n2, N1, and N2. When building multivariate prediction models, highly correlated predictors will lead to a high mul￾ticollinearity and hence might lead to inaccurate coefficient estimates [61]. Therefore, our study only takes into account n1, n2, N1, and N2. The process metrics consist of three rela￾tive code churn metrics, i.e. the normalized number of added, deleted, and modified source lines of code. These code churn metrics assume that a function with more added, deleted, or modified code would have a higher possibility of being fault-prone. The reasons for choosing these baseline code and process metrics in this study are three-fold. First, they are widely used product and process metrics in both industry and academic research [22], [23], [24], [25], [26], [27], [28], [29], [50], [52], [54], [55], [64]. Second, they can be automatically and cheaply collected from source code even for very large software systems. Third, many studies show that they are useful indicators for fault-proneness prediction [26], [27], [28], [50], [52], [54], [55], [64]. In the context of effort-aware post-release fault-proneness prediction, we believe that slice-based cohesion metrics are of practical value only if: (1) they have a significantly better fault-proneness predic￾tion ability than the baseline code and process metrics; or (2) they can significantly improve the performance of fault￾proneness prediction when used together with the baseline code and process metrics. This is especially true when con￾sidering the expenses for collecting slice-based cohesion metrics. As Meyers and Binkley stated [13], slicing techni￾ques and tools are now mature enough to allow an intensive empirical investigation. In our study, we use Frama-C, a well-known open-source static analysis tool for C programs [57], to collect slice-based cohesion metrics. Frama-C pro￾vides scalable and sound software analyses for C programs, thus allowing accurate collection of slice-based cohesion metrics on industrial-size systems [57]. 3 RESEARCH METHODOLOGY In this section, we first give the research hypotheses relating slice-based cohesion metrics to the most commonly used code and process metrics and to fault-proneness. Then, we describe the investigated dependent and independent variables, the employed modeling technique, and the data analysis methods. 3.1 Research Hypotheses The first research question (RQ1) of this study investigates whether slice-based cohesion metrics are redundant when compared with the most commonly used code and process metrics. It is widely believed that software quality cannot be measured using only a single dimension [29]. As stated in Section 2.2, the most commonly used code and process metrics measure software quality from size, control flow structure, and cognitive psychology perspectives. However, slice-based cohesion metrics measure software quality from the perspective of cohesion, which are based on control-/ data-flow dependence information among statements. Our conjecture is that, given the nature of the information and counting mechanism employed by slice-based cohesion metrics, they should capture different underlying dimen￾sions of software quality than the most commonly used code and process metrics capture. From this reasoning, we set up the following null hypothesis H10 and alternative hypothesis H1A for RQ1: H10. Slice-based cohesion metrics do not capture additional dimensions of software quality compared with the most commonly used code and process metrics. H1A. Slice-based cohesion metrics capture additional dimensions of software quality compared with the most commonly used code and process metrics. The second research question (RQ2) of this study investi￾gates whether slice-based cohesion metrics are statistically related to post-release fault-proneness. In the software engineering literature, there is a common belief that low cohesion indicates an inappropriate design [1], [2]. Conse￾quently, a function with low cohesion is more likely to be fault-prone than a function with high cohesion [1], [2]. From Section 2.1, we can see that slice-based cohesion metrics leverage the commonality among the slices with respect to different output variables of a function to quantify its cohesion. Existing studies showed that they provided an TABLE 3 Data-Token Level Slice Occurrence Matrix with Respect to End Slice Profile and Metric Slice Profile End slice Metric slice Line Token largest smallest range largest smallest range 1 A1 1 11 1 11 2 size1 1 11 1 11 3 largest1 1 01 1 01 4 smallest1 1 11 1 11 5 i1 1 11 1 11 6 range1 0 01 0 01 7 i2 1 11 1 11 7 11 1 11 1 11 8 range2 0 00 0 00 8 01 0 00 0 00 9 smallest2 1 11 1 11 9 A2 1 11 1 11 9 02 1 11 1 11 10 largest2 1 01 1 11 10 smallest3 1 01 1 11 11 i3 1 11 1 11 11 size2 1 11 1 11 12 smallest4 0 11 0 11 12 A3 0 11 0 11 12 i4 0 11 0 11 13 smallest5 0 11 0 11 13 A4 0 11 0 11 13 i5 0 11 0 11 14 largest3 1 01 1 11 14 A5 1 01 1 11 14 i6 1 01 1 11 15 largest4 1 01 1 11 15 A6 1 01 1 11 15 i7 1 01 1 11 16 i8 1 11 1 11 17 range3 0 01 1 11 17 largest5 0 01 1 11 17 smallest6 0 01 1 11 18 range4 0 01 1 11 336 IEEE TRANSACTIONS ON SOFTWARE ENGINEERING, VOL. 41, NO. 4, APRIL 2015