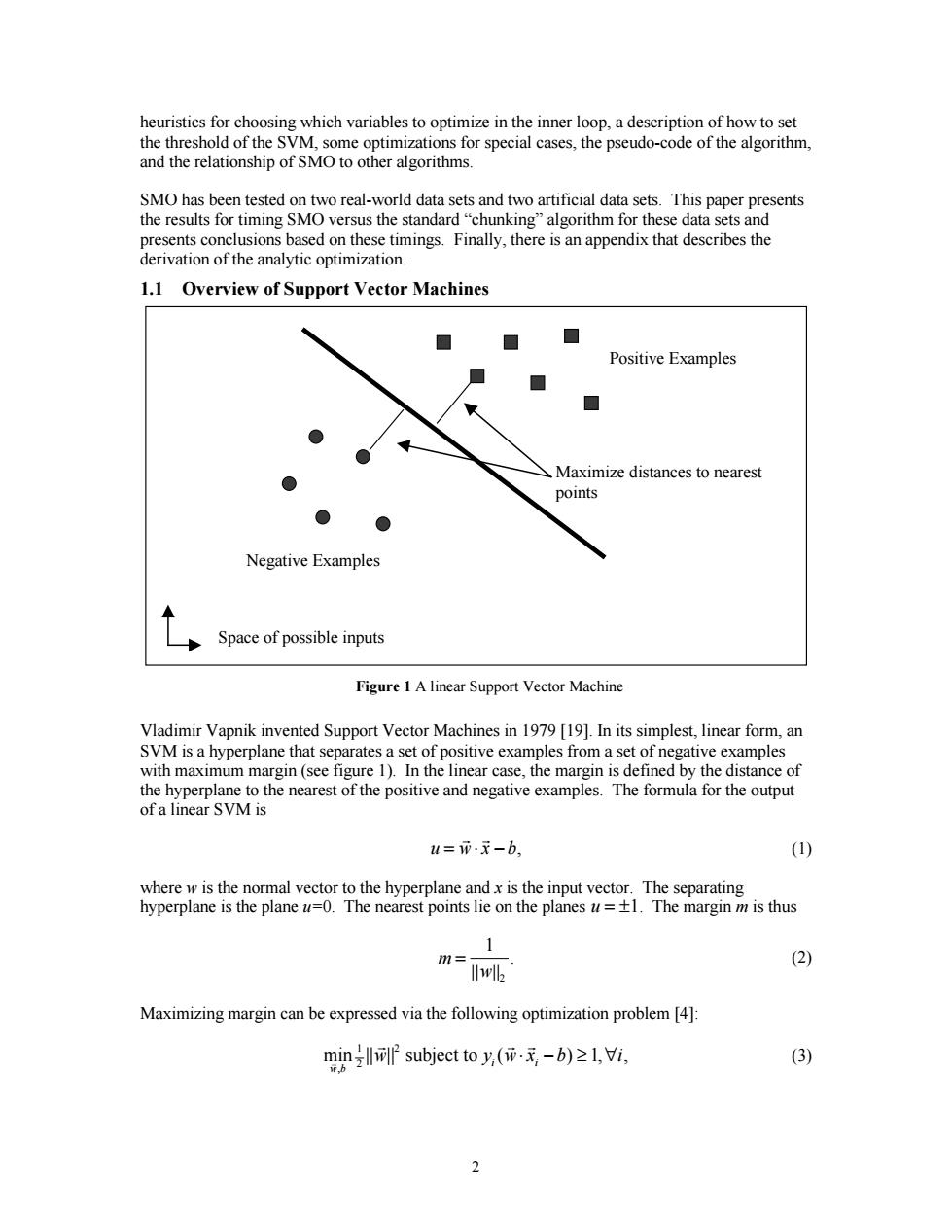
heuristics for choosing which variables to optimize in the inner loop,a description of how to set the threshold of the SVM,some optimizations for special cases,the pseudo-code of the algorithm, and the relationship of SMO to other algorithms. SMO has been tested on two real-world data sets and two artificial data sets.This paper presents the results for timing SMO versus the standard "chunking"algorithm for these data sets and presents conclusions based on these timings.Finally,there is an appendix that describes the derivation of the analytic optimization. 1.1 Overview of Support Vector Machines Positive Examples Maximize distances to nearest points Negative Examples Space of possible inputs Figure 1 A linear Support Vector Machine Vladimir Vapnik invented Support Vector Machines in 1979 [19].In its simplest,linear form,an SVM is a hyperplane that separates a set of positive examples from a set of negative examples with maximum margin(see figure 1).In the linear case,the margin is defined by the distance of the hyperplane to the nearest of the positive and negative examples.The formula for the output of a linear SVM is u=币.元-b, (1) where w is the normal vector to the hyperplane and x is the input vector.The separating hyperplane is the plane u=0.The nearest points lie on the planes u=+1.The margin m is thus m= (2) Iwlb Maximizing margin can be expressed via the following optimization problem [4]: min subject to y,(m.元-b)≥l,i, (3) wb 22 heuristics for choosing which variables to optimize in the inner loop, a description of how to set the threshold of the SVM, some optimizations for special cases, the pseudo-code of the algorithm, and the relationship of SMO to other algorithms. SMO has been tested on two real-world data sets and two artificial data sets. This paper presents the results for timing SMO versus the standard “chunking” algorithm for these data sets and presents conclusions based on these timings. Finally, there is an appendix that describes the derivation of the analytic optimization. 1.1 Overview of Support Vector Machines Vladimir Vapnik invented Support Vector Machines in 1979 [19]. In its simplest, linear form, an SVM is a hyperplane that separates a set of positive examples from a set of negative examples with maximum margin (see figure 1). In the linear case, the margin is defined by the distance of the hyperplane to the nearest of the positive and negative examples. The formula for the output of a linear SVM is u wx b = ⋅− r r , (1) where w is the normal vector to the hyperplane and x is the input vector. The separating hyperplane is the plane u=0. The nearest points lie on the planes u = ±1. The margin m is thus m w = 1 2 || || . (2) Maximizing margin can be expressed via the following optimization problem [4]: min || || ( ) , , , r r rr w b w y wx b i i i 1 2 2 subject to ⋅ − ≥∀1 (3) Positive Examples Negative Examples Maximize distances to nearest points Space of possible inputs Figure 1 A linear Support Vector Machine