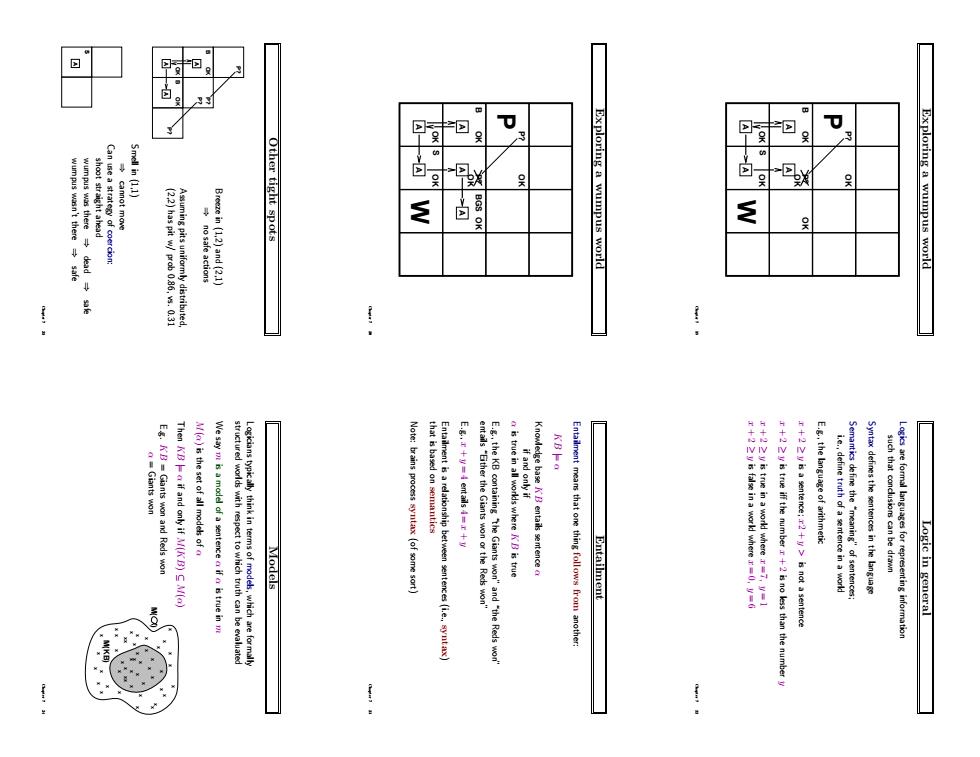
0 9 n pus shoot straight ahead Can ue a strategy of coercion: cannot move Other tight spots Exploring a wumpus world Exploring a wumpus world ThenKBa if and only if M(KB)C M(a) Note:brains pocess(ofm sort) that is based on semantics E.g.+y=4 entails4=r+y Egthe language of arithmetic Models Entailment +2i true iff the number+is no lss than the number Syntax defnesthes intheangug Logic in generalExploring a wumpus world OK OK OK A A B P? P? A S OK P W A OK OK Chapter 7 19 Exploring a wumpus world OK OK OK A A B P? P? A S OK P W A OK OK A BGS Chapter 7 20 Other tight spots A B OK OK OK A B A P? P? P? P? Breeze in (1,2) and (2,1) ⇒ no safe actions Assuming pits uniformly distributed, (2,2) has pit w/ prob 0.86, vs. 0.31 A S Smell in (1,1) ⇒ cannot move Can use a strategy of coercion: shoot straight ahead wumpus was there ⇒ dead ⇒ safe wumpus wasn’t there ⇒ safe Chapter 7 21 Logic in general Logics are formal languages for representing information such that conclusions can be drawn Syntax defines the sentences in the language Semantics define the “meaning” of sentences; i.e., define truth of a sentence in a world E.g., the language of arithmetic x + 2 ≥ y is a sentence; x2 + y > is not a sentence x + 2 ≥ y is true iff the number x + 2 is no less than the number y x + 2 ≥ y is true in a world where x = 7, y = 1 x + 2 ≥ y is false in a world where x = 0, y = 6 Chapter 7 22 Entailment Entailment means that one thing follows from another: KB |= α Knowledge base KB entails sentence α if and only if α is true in all worlds where KB is true E.g., the KB containing “the Giants won” and “the Reds won” entails “Either the Giants won or the Reds won” E.g., x + y = 4 entails 4 = x + y Entailment is a relationship between sentences (i.e., syntax) that is based on semantics Note: brains process syntax (of some sort) Chapter 7 23 Models Logicians typically think in terms of models, which are formally structured worlds with respect to which truth can be evaluated We say m is a model of a sentence α if α is true in m M(α) is the set of all models of α Then KB |= α if and only if M(KB) ⊆ M(α) E.g. KB = Giants won and Reds won α = Giants won M( ) M(KB) x x x x x x x x x x x x x x x x x x x x x x x x x xx x x x x x x x x x x x x x x x x x x x x Chapter 7 24