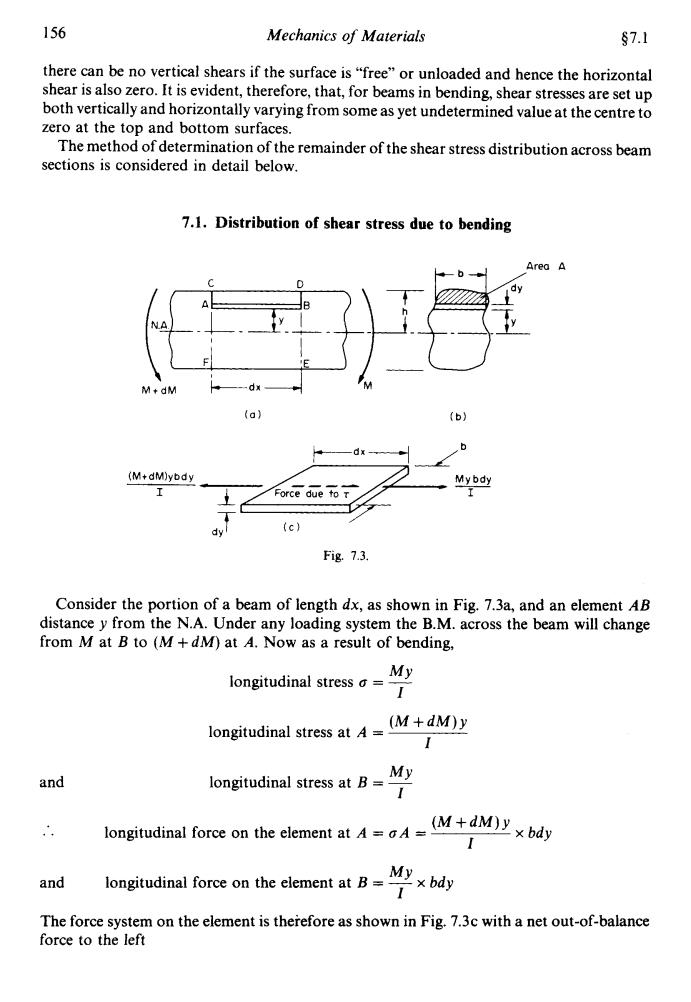
156 Mechanics of Materials 67.1 there can be no vertical shears if the surface is "free"or unloaded and hence the horizontal shear is also zero.It is evident,therefore,that,for beams in bending,shear stresses are set up both vertically and horizontally varying from some as yet undetermined value at the centre to zero at the top and bottom surfaces. The method of determination of the remainder of the shear stress distribution across beam sections is considered in detail below. 7.1.Distribution of shear stress due to bending Area A NA M+dM -dx (a) (b》 (M+dM)ybdy My bdy Force due to r dy (c) Fig.7.3. Consider the portion of a beam of length dx,as shown in Fig.7.3a,and an element AB distance y from the N.A.Under any loading system the B.M.across the beam will change from M at B to (M+dM)at A.Now as a result of bending, longitudinal stress a= My 1 longitudinal stress at=(M+dM)y 1 and longitudinal stress at B-My longitudinal force on the element atMM)by My and longitudinal force on the element at B= x bdy The force system on the element is therefore as shown in Fig.7.3c with a net out-of-balance force to the left156 Mechanics of Materials $7.1 there can be no vertical shears if the surface is "free" or unloaded and hence the horizontal shear is also zero. It is evident, therefore, that, for beams in bending, shear stresses are set up both vertically and horizontally varying from some as yet undetermined value at the centre to zero at the top and bottom surfaces. The method of determination of the remainder of the shear stress distribution across beam sections is considered in detail below. 7.1. Distribution of shear stress due to bending C D // I I (Mt dM)ybd y I 1 I Fig. 1.3. Consider the portion of a beam of length dx, as shown in Fig. 7.3a, and an element AB distance y from the N.A. Under any loading system the B.M. across the beam will change from M at B to (A4 + dM) at A. Now as a result of bending, and .. longituLinr MY longitudinal stress o = - (M+dWY MY longitudinal stress at B = ~ I I longitudinal stress at A = I x ". (M+dWY I rce on the element at A = oA = Y MY and The force system on the element is therefore as shown in Fig. 7.3~ with a net out-of-balance force to the left longitudinal force on the element at B = - x bdy I